Машинное обучение для начинающих: создание нейронных сетей

Многослойный персептрон и его особенности

Однослойная нейронная сеть прямого распространения (персептрон) была первой моделью искусственной нейросети, которая появилась ещё в середине 20 века. Однослойность помогала в том, чтобы анализировать работу персептрона и узнавать его функции.

Однако она же уменьшала его мощность: для сложных вычислений персептрон почти не подходит, а его способность обучаться почти что равна нулю.

Так называемый многослойный персептрон имеет значительно больше возможностей. Однако тот факт, что он тоже относится к сети прямого распространения, заставляет отнести его скорее к примитивным нейросетям, чем к продвинутым (таким, как головной мозг).

Свойства многослойного персептрона

Главным свойством, которое отличает его от однослойного, является наличие нескольких слоёв вычислительных нейронов между входным и выходным слоем. У однослойного персептрона, как понятно из названия, такой слой один.

Вторым важным свойством многослойного персептрона можно назвать уже отмеченную выше однонаправленность (линейность): сигнал от входных нейронов через слои вычислительных чётко направляется к выходным нейронам, обратное движение невозможно.

Помимо этих двух главных свойств, существует ещё три дополнительных, которые напрямую связаны с подобным строением персептрона.

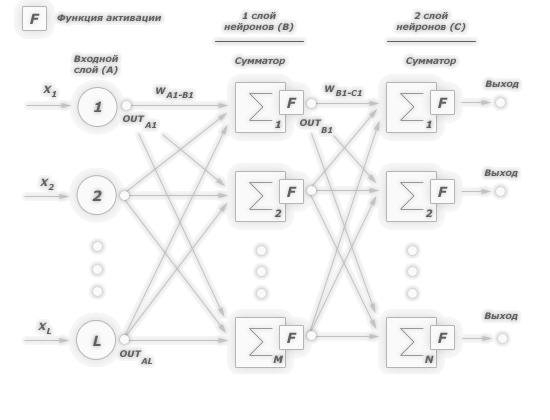
1. У каждого нейрона имеется своя функция активации.

Поскольку структура усложнена по сравнению с однослойной моделью, то появляется возможность отправлять сигналы с выхода каждого нейрона на один из нескольких соседствующих с ним. По этой причине функция активации, осуществляющая выбор нейрона и отправку на него сигнала, теперь является выделенной для каждого нейрона, в то время как в однослойной модели такая функция присутствует лишь у целого слоя.

2. Несколько слоёв нейронов открывают возможность для обучения сети.

Это одно из главных преимуществ данной модели, которое и обеспечило высокий интерес к ней со стороны исследователей.

3. Большое значение связей.

Межнейронные связи (синапсы) получают всё больше значения для многослойных нейросетей, и чем больше в них слоёв, тем выше значение таких связей.

Грамотная настройка весов для каждой межнейронной связи – важная, но сложная задача для разработчика подобной системы.

В целом многослойный персептрон имеет значительно больше возможностей, чем однослойный, однако понимание принципов его работы и предсказание результатов вычисления уже затруднено, хотя и не так сильно, как в случае с рекуррентными сетями (допускающими отправку промежуточных результатов снова на вход).

Evaluation

Lets classify the samples in our data set by hand now, to check if the perceptron learned properly:

First sample $(-2, 4)$, supposed to be negative:

Second sample $(4, 1)$, supposed to be negative:

Third sample $(1, 6)$, supposed to be positive:

Fourth sample $(2, 4)$, supposed to be positive:

Fifth sample $(6, 2)$, supposed to be positive:

Lets define two test samples now, to check how well our perceptron generalizes to unseen data:

First test sample $(2, 2)$, supposed to be negative:

Second test sample $(4, 3)$, supposed to be positive:

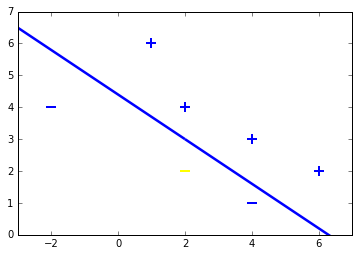
Both samples are classified right. To check this geometrically, lets plot the samples including test samples and the hyperplane.

Final Thoughts

Thats all about it. If you got so far, keep in mind, that the basic structure is the SGD applied to the objective function of the perceptron. This is just four lines of code. It contains all the learning magic. Cool isnt it?

I am looking forward for your comments.

Greetings from webstudio, Mavicc

A More Detailed Example

In this section I’m going to use a larger data set to train/test my Perceptron. I’ll also compare my results with an implementation from scikit-learn as a validation of my model.

Synthetic Dataset

In order to test my Perceptron for comparison with the scikit-learn implementation, I’m going to first create a dataset. Since I’ll be plotting the intercept, I’m going to put in a dummy feature in the first column, which will be ones. This way the model will learn the weights for the features, as well as the bias term for the intercept.

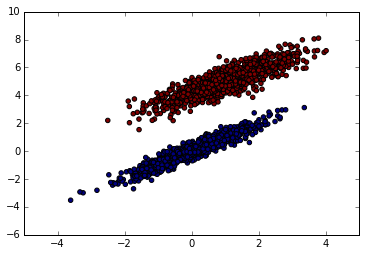
Splitting the Dataset

I didn’t split the data in the NAND example into training and test sets because I was just illustrating a simple example of the Perceptron algorithm. In this example I’m going to randomly sample 70% of the dataset for the training set, and predictions will be made on the remaining 30%. Splitting the dataset into training and test sets is good practice to try and avoid overfitting.

The next step is to train the model to determine the weights.

A plot of the model’s convergence is also useful.

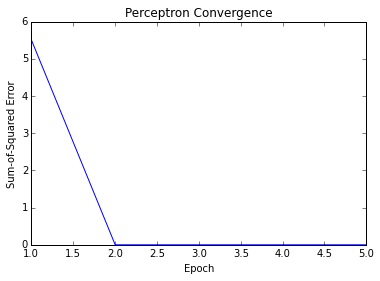
Testing the Model

Next, we’ll be testing the model.

We can see that the model performed perfectly. Since this is a pretty simple, linearly separable dataset, this isn’t surprising. Lets take a look at what the decision boundary looks like for this model.

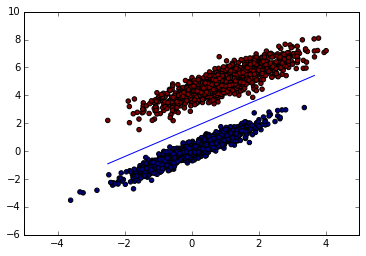
The plot of the decision boundary confirms that the model has clearly separated the two classes.

Scikit-learn Model

Based on the decision boundary, it looks like the model is working. Another good check is to verify it with a trusted implementation from scikit-learn. To compare the models, I’ll take a look at the weights for each model.

The scikit-learn implementation yielded identical weights to my model. This isn’t surprising given the clear separability of the two datasets.

I did have to manipulate a few details in the scikit-learn model though. I turned off the random state and the shuffle option so that the scikit-learn Perceptron would use the same random seed that I set for my model. I also set the learning rate to the same number as my perceptron. Finally, I turned of the fit_intercept option. Since I included the dummy column of ones in the dataset, I’m automatically fitting the intercept, so I don’t need this option turned on.

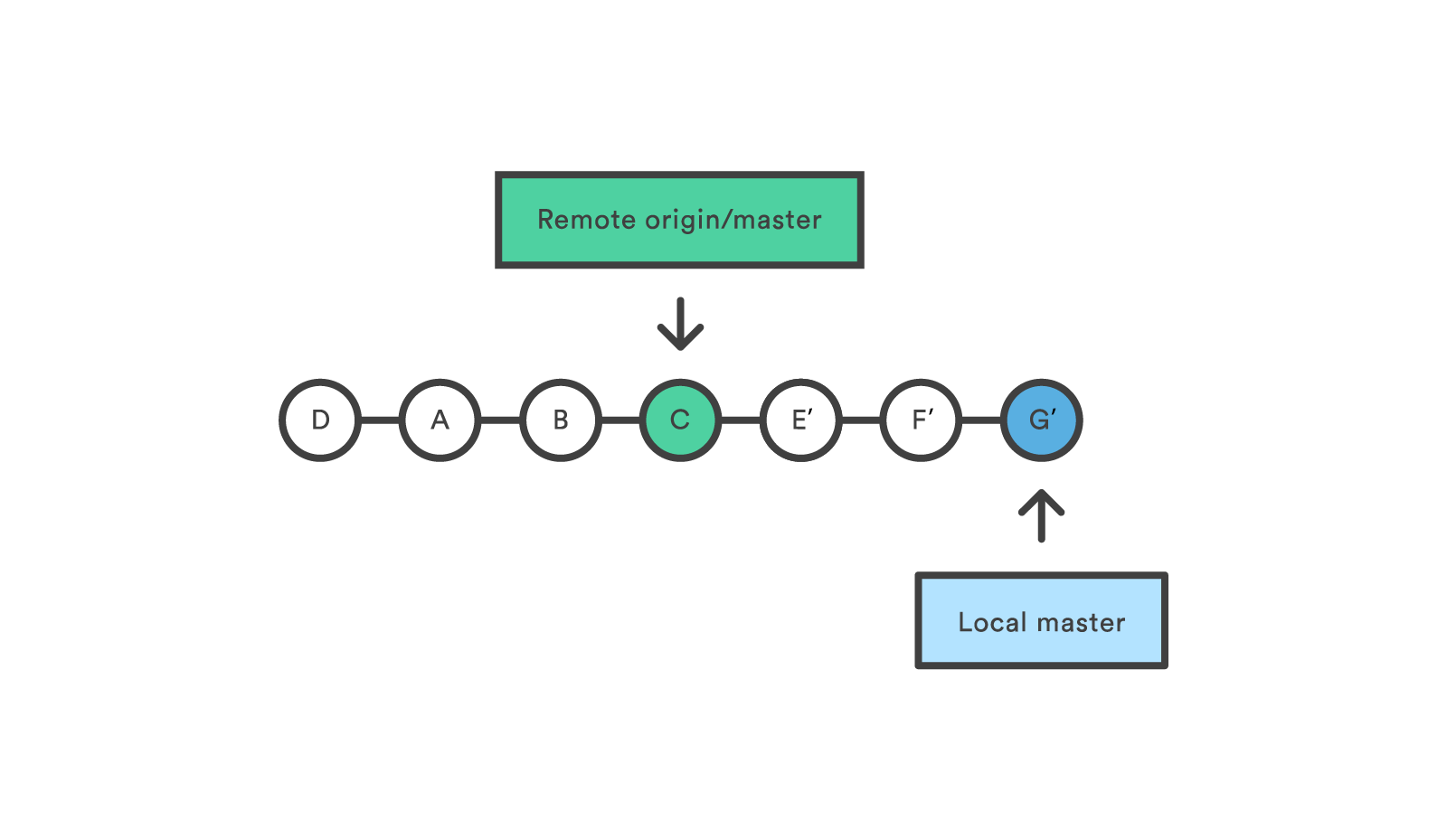
Обратное распространение

После того, как мы выполнили расчеты для прямого распространения, настало время изменить направление. Во фрагменте программы с обратным распространением мы перемещаемся к весам от скрытых узлов к выходному узлу, а затем к весам от входного слоя к скрытому слою, перенося при этом информацию об ошибке для эффективного обучения сети.

У нас есть два слоя для циклов : один для весовых коэффициентов между скрытым и выходным слоями и один для весовых коэффициентов между входным и скрытым слоями. Сначала мы генерируем сигнал ошибки (S_ошибки, ), который нам нужен для вычисления обоих градиентов, (от скрытого слоя к выходному) и (от входного слоя к скрытому), а затем мы обновляем весовые коэффициенты, вычитая градиент, умноженный на скорость обучения.

Обратите внимание, как веса между входным и скрытым слоями обновляются внутри цикла для значений между скрытым и выходным слоями. Мы начинаем с сигнала ошибки, который ведет обратно к одному из скрытых узлов, затем распространяем этот сигнал ошибки на все входные узлы, которые подключены к одному конкретному скрытому узлу:. Рисунок 2 – Обратное распространение ошибки

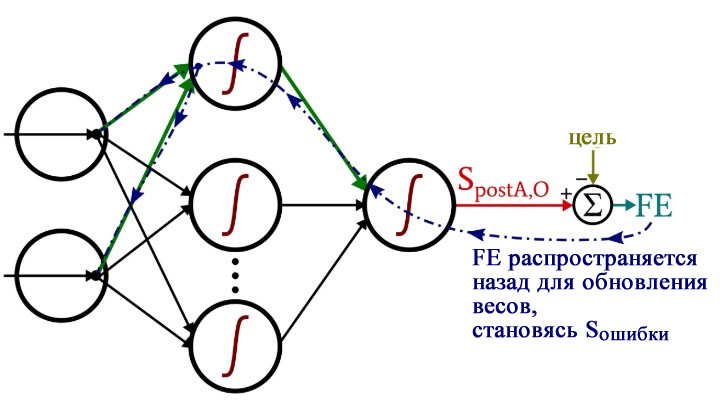Рисунок 2 – Обратное распространение ошибки

После того, как все весовые коэффициенты (как ItoH (от входного слоя к скрытому), так и HtoO (от скрытого слоя к выходному)), связанные с этим одним скрытым узлом, были обновлены, мы возвращаемся к началу и начинаем снова для следующего скрытого узла.

Также обратите внимание, что веса ItoH модифицируются перед весами HtoO. Мы используем текущий вес HtoO при расчете градиента, поэтому до выполнения расчетов мы не хотим изменять веса HtoO

Простейшая нейронная сеть

Сначала нужно подключить необходимые библиотеки, в нашем случае это . Я также отключаю вывод отладочных сообщений и работу с GPU, они нам не пригодятся. Для работы с массивами нам понадобится библиотека .

Теперь мы готовы создать нейросеть. Благодаря Tensorflow на это понадобится всего лишь четыре строчки кода.

Мы создали модель нейронной сети — класс — и добавили в нее два слоя: входной и выходной. Такая сеть называется «многослойный перцептрон» (multilayer perceptron), в общем виде она выглядит так.

Сеть multilayer perceptron

В нашем случае сеть имеет два входа (внешний слой), два нейрона во внутреннем слое и один выход.

Можно посмотреть, что у нас получилось:

Параметры сети

Обучение нейросети состоит в нахождении значений параметров этой сети.
Наша сеть имеет девять параметров. Чтобы обучить ее, нам понадобится исходный набор данных, в нашем случае это результаты работы функции .

Функция запускает алгоритм обучения, которое у нас будет выполняться тысячу раз, на каждой итерации параметры сети будут корректироваться. Наша сеть небольшая, так что обучение пройдет быстро. После обучения сетью уже можно пользоваться:

Результат соответствует тому, чему сеть обучалась.

Network test:
XOR(0,0): ]
XOR(0,1): ]
XOR(1,0): ]
XOR(1,1): ]

Мы можем вывести все значения найденных коэффициентов на экран.

Результат:

W1: ]
b1:
W2: ]
b2:

Внутренняя реализация функции выглядит примерно так:

Рассмотрим ситуацию, когда на вход сети подали значения :

L1 = X1W1 + b1 = =

Функция активации (rectified linear unit) — это просто замена отрицательных элементов нулем.

Теперь найденные значения попадают на второй слой.

L2 = X2W2 + b2 = 03.9633768 +2.9017112*3.9633768 + -4.897212 = 6.468379

Наконец, в качестве выхода используется функция , которая приводит значения к диапазону 0…1:

Мы совершили обычные операции умножения и сложения матриц и получили ответ: .

С этим примером на Python советую поэкспериментировать самостоятельно. Например, ты можешь менять число нейронов во внутреннем слое. Два нейрона, как в нашем случае, — это самый минимум, чтобы сеть работала.

Но алгоритм обучения, который используется в Keras, не идеален: нейросети не всегда удается обучиться за 1000 итераций, и результаты не всегда верны. Так, Keras инициализирует начальные значения случайными величинами, и при каждом запуске результат может отличаться. Моя сеть с двумя нейронами успешно обучалась лишь в 20% случаев. Неправильная работа сети выглядит примерно так:

XOR(0,0): ]
XOR(0,1): ]
XOR(1,0): ]
XOR(1,1): ]

Но это не страшно. Если видишь, что нейронная сеть во время обучения не выдает правильных результатов, алгоритм обучения можно запустить еще раз. Правильно обученную сеть потом можно использовать без ограничений.

Можно сделать сеть поумнее: использовать четыре нейрона вместо двух, для этого достаточно заменить строчку кода на . Такая сеть обучается уже в 60% случаев, а сеть из шести нейронов обучается с первого раза с вероятностью 90%.

Все параметры нейронной сети полностью определяются коэффициентами. Обучив сеть, можно записать параметры сети на диск, а потом использовать уже готовую обученную сеть. Этим мы будем активно пользоваться.

Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте

Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», увеличит личную накопительную скидку и позволит накапливать профессиональный рейтинг Xakep Score!
Подробнее

Вариант 2. Открой один материал

Заинтересовала статья, но нет возможности стать членом клуба «Xakep.ru»? Тогда этот вариант для тебя!
Обрати внимание: этот способ подходит только для статей, опубликованных более двух месяцев назад.

Я уже участник «Xakep.ru»

Тренировка нейронной сети — многовариантные исчисления, Часть 2

Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?

Для простоты давайте представим, что в наборе данных рассматривается только :

Имя/Name	Вес/Weight (минус 135)	Рост/Height (минус 66)	Пол/Gender
Alice	-2	-1	1

Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для :

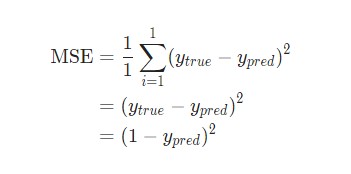
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:

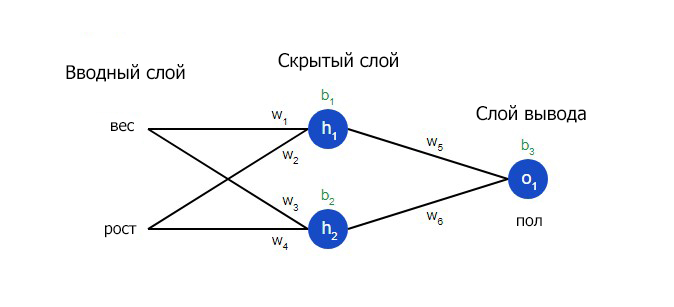
Затем можно прописать потерю как многовариантную функцию:

Представим, что нам нужно немного отредактировать . В таком случае, как изменится потеря после внесения поправок в ?

На этот вопрос может ответить частная производная . Как же ее вычислить?

Для начала, давайте перепишем частную производную в контексте :

Данные вычисления возможны благодаря дифференцированию сложной функции. 

Подсчитать можно благодаря вычисленной выше :

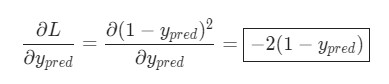
Теперь, давайте определим, что делать с . Как и ранее, позволим , , стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:

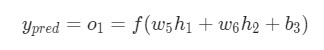Как было указано ранее, здесь является функцией активации сигмоида.

Так как влияет только на , а не на , можно записать:

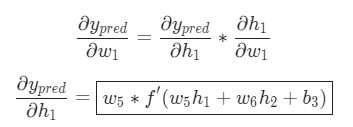Использование дифференцирования сложной функции.

Те же самые действия проводятся для :

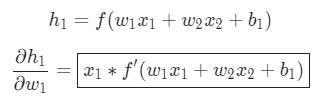Еще одно использование дифференцирования сложной функции.

В данном случае — вес, а — рост. Здесь как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:

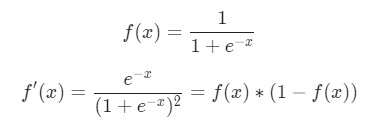
Функция в таком виде будет использована несколько позже.

Вот и все. Теперь разбита на несколько частей, которые будут оптимальны для подсчета:

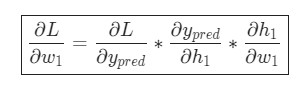
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.

У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.

Алгоритмы обучения

Важным свойством любой нейронной сети является способность к обучению. Процесс обучения является процедурой настройки весов и порогов с целью уменьшения разницы между желаемыми (целевыми) и получаемыми векторами на выходе. В своей книге Розенблат пытался классифицировать различные алгоритмы обучения персептрона, называя их системами подкрепления.

Система подкрепление — это любой набор правил, на основании которых можно менять с течением времени матрицу взаимодействия (или состояние памяти) персептрона.

Описывая эти системы подкрепления и уточняя возможные их виды, Розенблат основывался на идеях Д. Хебба об обучении, предложенных им в 1949 году, которые можно перефразировать в следующее правило, которое состоит из двух частей:

• Если два нейроны с обеих сторон синапса (соединения) активизируются одновременно (то есть синхронно), то прочность этого соединения возрастает.
• Если два нейроны с обеих сторон синапса активизируются асинхронно, то такой синапс ослабляется или вообще отмирает.

Обучение с учителем

Классический метод обучения персептрона — это метод коррекции ошибки. Он представляет собой такой вид обучения с учителем, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.

Допустим, мы хотим научить перцептрон разделять два класса объектов так, чтобы при предъявлении объектов первого класса выход перцептрона был положительный (1), а при предъявлении объектов второго класса — отрицательным (-1). Для этого выполним следующий алгоритм:

1. Случайно выбираем пороги для A-элементов и устанавливаем связи SA (далее они не будут меняться).
2. Начальные коэффициенты считаем равными нулю.
3. Предъявляем обучающую выборку: объекты (например, круги или квадраты) с указанием класса, к которому они принадлежат.
   • Показываем перцептроны объект первого класса. При этом некоторые A-элементы пробудятся. Коэффициенты, соответствующие этим возбуждением элементов, увеличиваем на 1.
   • Предъявляем объект второго класса, и коэффициенты тех А-элементов, которые возбудились при этом показе, уменьшаем на 1.
4. Обе части шага 3 выполним для всей обучающей выборки. В результате обучения сформируются значения весов связей.

Теорема сходимости персептрона, описана и доказана Ф. Розенблат (при участии Блока, Джозефа, Кести и других исследователей, которые работали вместе с ним), показывает, что элементарный перцептрон, обученный по такому алгоритму, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведет к достижению решения по конечный промежуток времени.

Обучение без учителя

Кроме классического метода обучения персептрона, Розенблат также ввел понятие об обучении без учителя, предложив следующий способ обучения:

Альфа-система подкрепления — это система подкрепления, при которой веса всех активных связей, ведущих к элементу, изменяются на одинаковую величину r, а веса неактивных связей за это время не меняются.

Позже, с разработкой понятия многослойного персептрона, альфа-система была модифицирована, и ее стали называть дельта-правилом. Модификацию было проведено с целью сделать функцию обучения дифференцируемой (например, сигмоидною), что в свою очередь требуется для применения метода градиентного спуска, благодаря которому возможно обучение более одного слоя.

Метод обратного распространения ошибки

Для обучения многослойных сетей ряд ученых, в том числе Д. Румельхартом, было предложено градиентный алгоритм обучения с учителем, который проводит сигнал ошибки, исчисленный выходами перцептрона, к его входов, слой за слоем. Сейчас это самый популярный метод обучения многослойных перцептронов. Его преимущество в том, что он может научить все слои нейронной сети, и его легко просчитать локально. Однако этот метод является очень длинным, к тому же, для его применения требуется, чтобы передаточная функция нейронов была дифференцируемой. При этом в перцептронах пришлось отказаться от бинарного сигнала, и пользоваться на входе непрерывными значениями.

Константы

Как и в случае с модификаторами доступа питон не пытается ограничить разработчика, поэтому задачать скалярную переменную защищённую от модификации стандартным способом нельзя, просто есть соглашение, что переменные с именем в верхнем регистре нужно считать константами.
С другой стороны в питоне есть неизменяемые структуры данных такие как tuple, поэтому если вы хотите сделать неизменяемой какую-то глобальную структуру вроде конфига и не хотите дополнительных зависимостей, то namedtuple, вполне хороший выбор, хотя он потребует немного больше усилий для описания типов, поэтому мне нравится альтернативная реализация неизменяемой структуры с dot-notation — Box (см. параметр frozen_box).
Ну а если вам хочется скалярных констант, то можно реализовать проверку доступа к ним на стадии «компиляции» т.е. проверки через mypy, пример и .

Решение задач с помощью перцептрона

В предыдущем разделе я описал наш перцептрон как инструмент для решения задач. Однако вы, возможно, заметили, что этот перцептрон не сильно занимался решением задач – я решил задачу и дал решение перцептрону, назначив требуемые веса.

К этому моменту мы достигли ключевой концепции нейронной сети: я смог быстро решить проблему классификации действительные/недействительные, потому что связь между входными данными и искомыми выходными значениями очень проста. Однако во многих реальных ситуациях человеку было бы чрезвычайно трудно сформулировать математическую связь между входными данными и выходными значениями. Мы можем получать входные данные и записывать или производить соответствующие выходные значения, но у нас нет математического маршрута от входа к выходу.

Полезным примером является распознавание рукописного текста. Допустим, у нас есть изображения рукописных символов, и мы хотим классифицировать эти изображения как «a», «b», «c» и т.д., чтобы мы могли преобразовать рукописный текст в обычный компьютерный текст. Любой, кто знает, как писать и читать, сможет генерировать входные изображения и затем назначать правильные категории для каждого изображения. Таким образом, сбор входных данных и соответствующих выходных данных не представляет трудностей. С другой стороны, было бы чрезвычайно сложно взглянуть на пары вход-выход и сформулировать математическое выражение или алгоритм, который бы правильно преобразовывал входные изображения в выходную категорию.

Таким образом, распознавание рукописного текста и многие другие задачи обработки сигналов представляют собой математические задачи, которые люди не могут решить без помощи сложных инструментов. Несмотря на то, что нейронные сети не могут мыслить, анализировать и вводить новшества, они позволяют нам решать эти сложные задачи, потому что они могут делать то, чего не могут люди, то есть быстро и многократно выполнять вычисления с использованием потенциально огромного количества числовых данных.

Обучение нейросети

Процесс, который позволяет нейронной сети создавать математический маршрут от входа к выходу, называется обучением. Мы даем данные для обучения сети, состоящие из входных значений и соответствующих выходных значений, и к этим значениям применяется фиксированная математическая процедура. Целью этой процедуры является постепенное изменение весов сети таким образом, чтобы сеть могла рассчитывать правильные выходные значения даже с входными данными, которые она никогда раньше не видела. По сути, это поиск шаблонов в обучающих данных и генерация весов, которые позволят получить полезный результат путем применения этих шаблонов к новым данным.

На следующей диаграмме показан рассмотренный выше классификатор действительный/недействительный, но веса различаются. Это веса, которые я сгенерировал, тренируя перцептрон с помощью 1000 точек данных. Как видите, процесс обучения позволил перцептрону автоматически аппроксимировать математические связи, которые я определил с помощью критического мышления в человеческом стиле.

Рисунок 4 – Результаты обучения нейросети перцептрон

Примечания

1. Parallel Distributed Processing: Explorations in the Microstructures of Cognition / Ed. by Rumelhart D. E. and McClelland J. L.— Cambridge, MA: MIT Press, 1986.
2. Обучение машины классификации объектов, Аркадьев А. Г., Браверман Э. М., Изд-во «Наука», Главная редакция физико-математической литературы, М., 1971, 192 стр.
3. S. Jakovlev. Архитектура перцептрона, обеспечивающая компактность описания образов = Perceptron architecture ensuring pattern description compactnes // Scientific proceedings of Riga Technical University, RTU. — Riga, 2009.
4. Werbos P. J. 1974. Beyond regression: New tools for prediction and analysis in the behavioral sciences. PhD thesis, Harward University
5. Галушкин А.И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
6. Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
7. Уоссермен, Ф. Нейрокомпьютерная техника: Теория и практика = Neural Computing. Theory and Practice. — М.: Мир, 1992. — 240 с.

Что такое Keras?

Keras — это библиотека для Python с открытым исходным кодом, которая позволяет легко создавать нейронные сети. Библиотека совместима с TensorFlow, Microsoft Cognitive Toolkit, Theano и MXNet. Tensorflow и Theano являются наиболее часто используемыми численными платформами на Python для разработки алгоритмов глубокого обучения, но они довольно сложны в использовании.

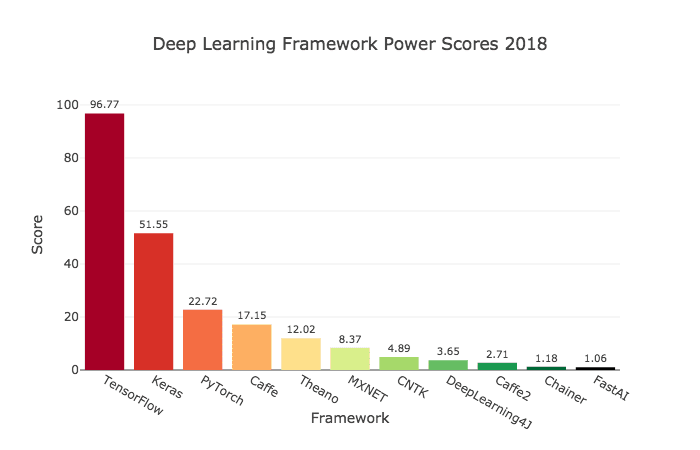Оценка популярности фреймворков машинного обучения по 7 категориям

Читайте: TensorFlow туториал. Часть 1: тензоры и векторы

Keras, наоборот, предоставляет простой и удобный способ создания моделей глубокого обучения. Ее создатель, François Chollet, разработал ее для того, чтобы максимально ускорить и упростить процесс создания нейронных сетей

Он сосредоточил свое внимание на расширяемости, модульности, минимализме и поддержке Python. Keras можно использовать с GPU и CPU; она поддерживает как Python 2, так и Python 3

Keras компании Google внесла большой вклад в коммерциализацию глубокого обучения и искусственного интеллекта, поскольку она содержит cовременные алгоритмы глубокого обучения, которые ранее были не только недоступными, но и непригодными для использования.

Отличия многослойного перцептрона от перцептрона Розенблатта

В 1988 году Минский переиздал книгу «Перцептроны», в которую включил новые главы. В них, в частности, анализируются отличия между обучением перцептрона методом коррекции ошибки и обучением многослойного перцептрона Румельхарта методом обратного распространения ошибки. Минский показал, что качественно отличий нет, оба способа решают сопоставимые задачи и с той же эффективностью и ограничениями. Разница лишь в способе достижения решения.

Среди отличий многослойного перцептрона Румельхарта от перцептрона Розенблатта можно выделить следующие:

• Использование нелинейной функции активации, как правило сигмоидальной.
• Число обучаемых слоев больше одного. Чаще всего в приложениях используется не более трёх.
• Сигналы, поступающие на вход и получаемые с выхода, не бинарные, а могут кодироваться десятичными числами, которые нужно нормализовать так, чтобы значения были на отрезке от 0 до 1 (нормализация необходима как минимум для выходных данных, в соответствии с функцией активации — сигмоидой).
• Допускается произвольная архитектура связей (в том числе, и полносвязные сети).
• Ошибка сети вычисляется не как число неправильных образов после итерации обучения, а как некоторая статистическая мера невязки между нужным и получаемым значением.
• Обучение проводится не до отсутствия ошибок после обучения, а до стабилизации весовых коэффициентов при обучении или прерывается ранее, чтобы избежать переобучения.

Многослойный перцептрон будет обладать функциональными преимуществами по сравнению с перцептроном Розенблатта только в том случае, если в ответ на стимулы не просто будет выполнена какая-то реакция (поскольку уже в перцептроне может быть получена реакция любого типа), а выразится в повышении эффективности выработки таких реакций. Например, улучшится способность к обобщению, то есть к правильным реакциям на стимулы которым перцептрон не обучался. Но на данный момент таких обобщающих теорем нет, существует лишь масса исследований различных стандартизированных тестов, на которых сравниваются различные архитектуры.

Терминология

Эта тема быстро станет неуправляемой, если мы не будем придерживаться четкой терминологии. Я буду использовать следующие термины:

• Преактивация (сокращенно \(S_{preA}\)): Это относится к сигналу (на самом деле это просто число в контексте одной обучающей итерации), который служит входным для функции активации узла. Он рассчитывается путем выполнения скалярного произведения массива, содержащего веса, и массива, содержащего значения, исходящие из узлов в предыдущем слое. Скалярное произведение эквивалентно выполнению поэлементного умножения двух массивов и затем суммированию элементов массив, полученного в результате этого умножения.
• Постактивация (сокращенно \(S_{postA}\)): Это относится к сигналу (опять же, просто число в контексте отдельной итерации), который выходит из узла. Он создается путем применения функции активации к сигналу преактивации. Я предпочитаю обозначение функции активации \(f_{A}()\), это логистическая сигмоидная функция.
• В коде на Python вы увидите весовые матрицы, помеченные как ItoH и HtoO. Я использую эти идентификаторы, потому что фраза «веса скрытого слоя» будет неоднозначной – это будут веса, которые применяются до или после скрытого слоя? В моей схеме ItoH указывает веса, которые применяются к значениям, передаваемым из входных узлов в скрытые узлы (ItoH – Input toHidden), а HtoO определяет веса, которые применяются к значениям, передаваемым из скрытых узлов в выходной узел (HtoO – Hidden toOutput).
• Правильное выходное значение для обучающей выборки называется целью и обозначается буквой T (Target).
• Скорость обучения сокращенно обозначается как LR (Learning Rate).
• Конечная ошибка (FE – Final Error) – это разница между сигналом постактивации от выходного узла (\(S_{postA,O}\)) и целью, рассчитывается как \(FE = S_{postA,O}-T\).
• Сигнал ошибки (\(S_{ошибки}\)) – это последняя ошибка, распространяемая обратно к скрытому слою через функцию активации выходного узла.
• Градиент представляет вклад заданного веса в сигнал ошибки. Мы изменяем веса, вычитая этот вклад (умноженный на скорость обучения, если необходимо).

Некоторые из этих терминов показаны на следующей диаграмме конфигурации нейросети. Я знаю, это выглядит как разноцветный бардак. Приношу извинения. Это насыщенная информацией диаграмма, и, если вы внимательно ее изучите, я думаю, что вы найдете ее очень полезной.

Рисунок 2 – Демонстрация терминов на диаграмме конфигурации нейросети

Формулы обновления весовых коэффициентов получаются путем взятия частной производной функции ошибки (мы используем среднюю квадратичную ошибку) относительно веса, который необходимо изменить. Если вы хотите посмотреть математику, обратитесь к посту доктора Стэнсбери; в данной статье мы перейдем непосредственно к результатам. Для весов от скрытых узлов к выходным узлам (HtoO) мы имеем следующее:

\

\

\

Мы рассчитываем сигнал ошибки путем умножения конечной ошибки на значение, которое получается, когда мы берем производную функции активации по сигналу преактивации, доставляемому на выходной узел (обратите внимание на штрих, который означает первую производную, в \({f_A}'(S_{preA,O})\)). Затем вычисляется градиент путем умножения сигнала ошибки на сигнал постактивации из скрытого слоя

Наконец, мы обновляем вес, вычитая этот градиент из текущего значения веса, и, если мы хотим изменить размер шага, то можем умножить градиент на скорость обучения.

Для весов от входных узлов к скрытым узлам (ItoH) мы имеем следующее:

\

\

\

Для весов от входных узлов к скрытым узлам ошибка должна распространяться обратно через дополнительный слой, и мы делаем это путем умножения сигнала ошибки на вес между скрытым и выходным узлами, соединенный с интересующим скрытым узлом. Таким образом, если мы обновляем вес между входным и скрытым узлами, который ведет к первому скрытому узлу, мы умножаем сигнал ошибки на вес, который соединяет первый скрытый узел с выходным узлом. Затем мы завершаем вычисление, выполняя умножения, аналогичные умножениям обновления весов между скрытыми и выходными узлами: мы берем производную функции активации по сигналу преактивации скрытого узла, а «входное» значение можно рассматривать как сигнал постактивации от входного узла.