Зоны френеля. просто о сложном

Интеграл Френеля

В скалярной теории дифракции распределение электрического поля дифрагирующего света в точке (x,y,z) задаётся выражением Релея-Зоммерфельда:

E(x,y,z)=−iλ∬−∞+∞E(x′,y′,)eikrrcos⁡θdx′dy′{\displaystyle E(x,y,z)=-{i \over \lambda }\iint _{-\infty }^{+\infty }{E(x’,y’,0){\frac {e^{ikr}}{r}}\cos \theta }dx’dy’}

где r=(x−x′)2+(y−y′)2+z2{\displaystyle r={\sqrt {(x-x’)^{2}+(y-y’)^{2}+z^{2}}}}, i{\displaystyle i} — мнимая единица, и cos⁡θ=zr{\displaystyle \cos \theta ={\frac {z}{r}}} — косинус угла между направлениями z и r. В аналитическом виде этот интеграл представим только для простейших геометрий отверстий, поэтому он вычисляется обычно численными методами.

Аппроксимация Френеля

Главная трудность при вычислении интеграла представляет собой выражение для r. Во-первых, упростим вычисления, сделав замену переменных:

ρ2=(x−x′)2+(y−y′)2{\displaystyle \rho ^{2}=(x-x’)^{2}+(y-y’)^{2}}

Подставляя это выражение вместо r, найдём:

r=ρ2+z2=z1+ρ2z2{\displaystyle r={\sqrt {\rho ^{2}+z^{2}}}=z{\sqrt {1+{\frac {\rho ^{2}}{z^{2}}}}}}

Воспользуемся разложением Тейлора в ряд

1+u=(1+u)12=1+u2−u28+⋯{\displaystyle {\sqrt {1+u}}=(1+u)^{1/2}=1+{\frac {u}{2}}-{\frac {u^{2}}{8}}+\cdots }

и выразим r в виде

r=z1+ρ2z2=z1+ρ22z2−18(ρ2z2)2+⋯=z+ρ22z−ρ48z3+⋯{\displaystyle r=z{\sqrt {1+{\frac {\rho ^{2}}{z^{2}}}}}=z\left=z+{\frac {\rho ^{2}}{2z}}-{\frac {\rho ^{4}}{8z^{3}}}+\cdots }

Если мы рассмотрим все члены разложения, это будет точным выражением. Подставим это выражение в аргумент экспоненциальной функции под интегралом; ключевую роль в приближении Френеля играет пренебрежение третьим членом в разложении, который предполагается малым. Чтобы это было возможным, он должен слабо влиять на показатель степени. Другими словами, он должен быть намного меньше, чем период показателя экспоненты, то есть 2π{\displaystyle 2\pi }:

kρ48z3≪2π.{\displaystyle k{\frac {\rho ^{4}}{8z^{3}}}\ll 2\pi .}

Выражая k в терминах длины волны,

k=2πλ{\displaystyle k={2\pi \over \lambda }}

получим следующее соотношение:

ρ4z3λ≪8{\displaystyle {\frac {\rho ^{4}}{z^{3}\lambda }}\ll 8}

Умножая обе стороны на zλ{\displaystyle z/\lambda }, получим

ρ4z2λ2≪8zλ{\displaystyle {\frac {\rho ^{4}}{z^{2}\lambda ^{2}}}\ll 8{z \over \lambda }}

или, подставляя ранее полученное выражение для ρ2,

(x−x′)2+(y−y′)22z2λ2≪8zλ{\displaystyle {\frac {^{2}}{z^{2}\lambda ^{2}}}\ll 8{z \over \lambda }}

Если это условие выполняется для всех значений x, x’ , y и y’ , тогда мы можем пренебречь третьим членом в разложении Тейлора. Более того, если третий член мал, то все последующие слагаемые более высоких порядков тоже малы, и ими можно пренебречь. Тогда можно аппроксимировать выражение, используя два члена разложения:

r≈z+(x−x′)2+(y−y′)22z{\displaystyle r\approx z+{\frac {(x-x’)^{2}+(y-y’)^{2}}{2z}}}

Это выражение называется приближением Френеля, а неравенство, полученное ранее, есть условие применимости этого приближения.

Дифракция Френеля

Условие применимости достаточно слабо и позволяет все характерные размеры взять как сравнимые величины, если апертура много меньше, чем длина пути. К тому же, так как нас интересует только малая область недалеко от источника, величины x и y много меньше, чем z, предположим θ≈{\displaystyle \theta \approx 0}, что означает cos⁡θ≈1{\displaystyle \cos \theta \approx 1}, и r в знаменателе можно аппроксимировать выражением r≈z{\displaystyle r\approx z}.

В противоположность дифракции Фраунгофера, дифракция Френеля должна учитывать кривизну волнового фронта, чтобы правильно учесть относительные фазы интерферирующих волн.

Электрическое поле для дифракции Френеля в точке (x,y,z) дано в виде:

E(x,y,z)=−iλeikzz∬−∞+∞E(x′,y′,)eik2z(x−x′)2+(y−y′)2dx′dy′{\displaystyle E(x,y,z)=-{i \over \lambda }{e^{ikz} \over z}\iint _{-\infty }^{+\infty }E(x’,y’,0)e^{{ik \over 2z}}dx’dy’}

Это — интеграл дифракции Френеля; он означает, что, если приближение Френеля действительно, распространяющееся поле — волна, начинающаяся в апертуре и движущаяся вдоль z. Интеграл модулирует амплитуду и фазу сферической волны. Аналитическое решение этого выражения возможно только в редких случаях. Для дальнейшего упрощения, действительного только для намного больших расстояний от источника дифракции, см. дифракция Фраунгофера.

Принцип Гюйгенса — Френеля

Принцип Гюйгенса-Френеля гласит, что каждая точка на волновом фронте является источником вейвлетов. Эти вейвлеты распространяются в прямом направлении с той же скоростью, что и исходная волна. Новый волновой фронт – это линия, касающаяся всех вейвлетов.

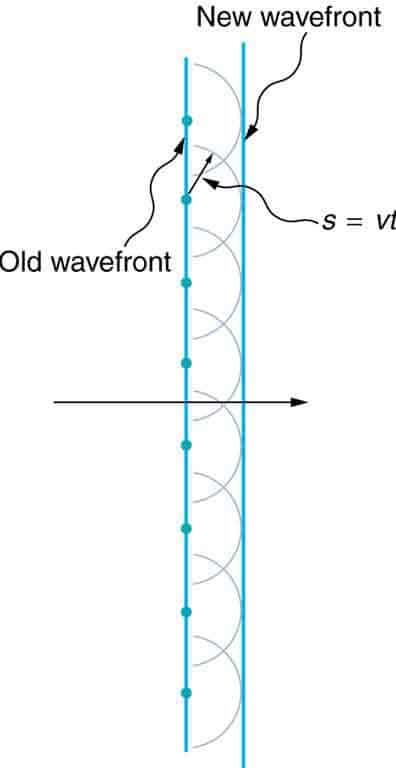Рис 3. Форма волны

Кристиан Гюйгенс был голландским ученым, который разработал полезную технику для определения того, как и где распространяются волны. В 1678 году он предположил, что каждая точка, к которой относится световое возмущение, сама становится источником сферической волны. Сумма вторичных волн (волн, являющихся результатом возмущения) определяет форму новой волны, показывает вторичные волны, идущие вперед от их источника. Он смог придумать объяснение линейного и сферического распространения волн и вывести законы отражения и преломления (описанные в предыдущих атомах), используя этот принцип. Однако он не мог объяснить то, что обычно называют дифракционными эффектами. Эффекты дифракции – это отклонения от прямолинейного распространения, которое возникает, когда свет сталкивается с краями, экранами и отверстиями.

Прямой волновой фронт: принцип Гюйгенса, применяемый к прямому волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние:

\

Новый волновой фронт представляет собой линию, касательную к вейвлетам.

Принцип Гюйгенса

На рисунке показан простой пример дифракционного принципа Гюйгенса. Принцип может быть показан с помощью уравнения ниже:

​\( s = Vts \)​

где s – расстояние, V – скорость распространения, а t – время.

Каждая точка на волновом фронте испускает волну со скоростью V. Испускаемые волны полукруглые и появляются в момент времени t. Новый волновой фронт касается вейвлетов. Этот принцип работает для всех типов волн, а не только для световых волн. Принцип полезен при описании отражения, преломления и интерференции. наглядно показывает, как принцип Гюйгенса может быть использован для объяснения отражения, и показывает, как его можно применять к преломлению.

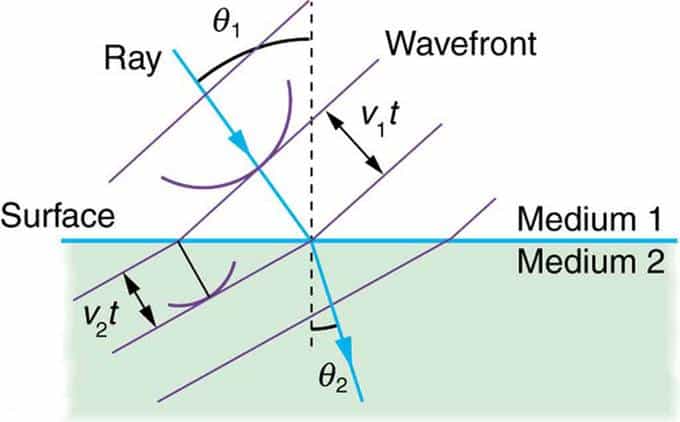Рис 4. Рефракционная составляющая

Рефракция Гюйгенса: принцип Гюйгенса применяется к прямому волновому фронту, перемещающемуся из одной среды в другую, где его скорость меньше. Луч изгибается в направлении перпендикуляра, поскольку вейвлеты имеют меньшую скорость во второй среде.

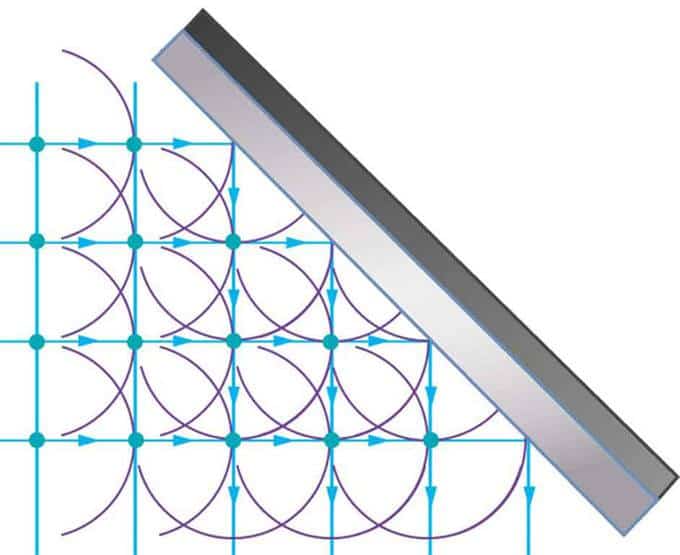Рис 4. Рефлекционная составляющая.

Отражение : принцип Гюйгенса применяется к прямому волновому фронту, ударяющемуся о зеркало. Показанные вейвлеты испускались, когда каждая точка на фронте волны ударялась о зеркало. Касательная к этим вейвлетам показывает, что новый волновой фронт был отражен под углом, равным углу падения. Направление распространения перпендикулярно фронту волны, как показано стрелками, направленными вниз.

Важность зон Френели

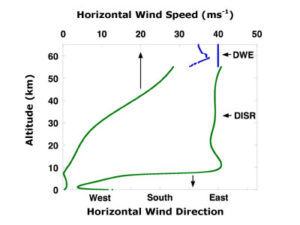
Если свободный, радиоволны поедут в прямой линии с передатчика на приемник. Но если есть рефлексивные поверхности вдоль пути, такие как массы воды или сглаживают ландшафт, радиоволны, размышляющие от тех поверхностей, могут прибыть или несовпадающие по фазе или в фазу с сигналами, которые едут непосредственно в приемник. Волны, которые размышляют прочь поверхностей в ровной зоне Френеля, не совпадают с волной прямого пути и уменьшают власть полученного сигнала. Волны, которые размышляют прочь поверхностей в странной зоне Френеля, совпадают с волной прямого пути и могут увеличить власть полученного сигнала. Иногда это приводит к парадоксальному открытию, что сокращение высоты антенны увеличивает отношение сигнал-шум.

Френель обеспечил средство вычислить, где зоны — где данное препятствие вызовет главным образом в фазе или главным образом несовпадающих по фазе размышлениях между передатчиком и приемником. Препятствия в первой зоне Френеля создадут сигналы с изменением фазы длины пути от 0 до 180 градусов во второй зоне, они будут 180 — 360 несовпадающими по фазе градусами и так далее. Четные зоны имеют максимальный эффект отмены фазы, и странные пронумерованные зоны могут фактически добавить к власти сигнала.

Чтобы максимизировать силу приемника, нужно минимизировать эффект потери преграды, удалив препятствия из угла обзора радиочастоты (RF LoS). Самые сильные сигналы находятся на прямой линии между передатчиком и приемником и всегда лежат в первой зоне Френеля.

Дифракция Френеля на круглом отверстии

Предположим, что монохроматический луч света падает на экран с круглым отверстием в нем. На определенном расстоянии от отверстия на втором экране можно наблюдать дифракционную картину. Структура рисунка зависит от длины волны, и распределение фаз входящего волнового фронта, а также по диаметру, отверстия и расстояния, от дыры до экрана.

В этом так называемом дифракционном режиме ближнего поля или Френеля монохроматическая плоская или сферическая волна, которая освещает отверстие, будет создавать дифракционную картину в виде набора концентрических колец. Излучение на оптической оси будет минимальным или максимальным, когда при постоянной длине волны и диаметре отверстия расстояние от отверстия до экрана наблюдения уменьшается от бесконечности до нуля.

Кольца появляются после прохождения критического расстояния (также называемого длиной Рэлея):

\( z_p = A \lambda Z_p = A \lambda \)

Если ​\( r > 3pZ>Z_p \)​– колец нет, но наблюдается плавное распределение освещенности в виде квадрата функции Бесселя, форма которого (но не диаметр пучка) остается постоянной при увеличении z. Это дальнее поле также называется дифракцией Фраунгофера.

То, появляется ли максимум или минимум на оптической оси, можно понять с помощью теории зон Френеля. Если число полу-лямбда-зон, «видимых» наблюдателем, нечетно, наблюдается максимум, четное количество зон создает минимальное излучение. Количество зон Френеля указывается номером Френеля:

​\( NF=Z_pZNF=Z_pZ \)​

В этих экспериментах измеряются расстояния, на которых появляются максимальная или минимальная интенсивность на оптической оси. Из этих измерений можно определить длину волны света, если известен диаметр отверстия.

В этом упражнении рассматриваются два входящих волновых фронта: плоская волна и сферическая волна.

Зоны Френеля для плоской волны

Рассмотрим разбивку площади отверстия на более тонкие кольца с равной площадью. Эти круги являются вторичными источниками света. Амплитуда световой волны, пришедшей от каждого кольца к наблюдателю, примерно одинакова. Кроме того, разность фаз от соседнего круга в точке Н также одинакова. В таком случае комплексные амплитуды в точке наблюдателя при сложении на единой комплексной плоскости образуют часть окружности – дугу. Суммарная же амплитуда – это хорда. Теперь рассмотрим, каким образом меняется картина суммирования комплексных амплитуд в случае изменения радиуса отверстия при условии сохранения остальных параметров задачи. В том случае, если отверстие открывает для наблюдателя всего одну зону, картина сложения будет представлена частью окружности. Амплитуда от последнего кольца будет повернута на угол π относительно центральной части, т. к. разность хода первой зоны, согласно определению, равна λ/2. Данный угол π будет означать, что амплитуды составят половину окружности. В таком случае сумма этих значений в точке наблюдения будет равна нулю – нулевая длина хорды. Если будет открыто три кольца, то картина представит собой полторы окружности и так далее. Амплитуда в точке наблюдателя для четного количества колец равна нулю. А в случае когда используют нечетное число кругов, она будет максимальной и равной значению длины диаметра на комплексной плоскости сложения амплитуд. Рассмотренные задачи в полной мере раскрывают метод зон Френеля.

Применение

Рассматриваемое утверждение дает возможность объяснить различные оптические явления:

• распространение светового излучения;
• дифракцию;
• интерференцию;
• отражение;
• преломление;
• двулучепреломление и другие.

С помощью принципа Гюйгенса-Френеля можно рассчитать амплитуду и интенсивность светового излучения. Для этого используются методы зон Френеля.

Зоны Френеля

Благодаря открытиям Гюйгенса и Френеля в таких задачах можно заменить один первичный источник совокупностью вторичных источников.

Это существенно облегчает задачу, например, для сферического случая. Такой метод расчета называется методом зон Френеля.

Сферический случай

Для сферического случая можно посчитать радиус зоны. Это внешний радиус кольца.

Площади зон Френеля с небольшими номерами примерно одинаковы. Они не зависят от номера зоны m. Они считаются как разница площадей сегментов сферы. Если не углубляться в детали, площади зон Френеля в этом случае находят так. Нужно умножить длину волны на радиус сферического волнового фронта R, на расстояние до точки наблюдения a и на число пи, а затем поделить на сумму R и a.

Зоны Френеля находят применение в зонных пластинках со светлыми и темными кольцами-радиусами, соответствующими размерам зон. Они работают аналогично собирающей линзе.

Дифракция

Пример — плоская волна, падающая на плоскость с отверстием. Когда она проходит через отверстие, все точки фронта излучают вторичные сферические колебания. С помощью построения огибающей увидим, что фронт волны оказывается там, куда согласно геометрической оптике свет попадать не должен.

Френель обосновал явление дифракции света по принципу Гюйгенса-Френеля и создал метод ее расчета. Развив принцип Гюйгенса, он установил, что:

• все участки волнового фронта колебания, исходящего из одной точки, когерентны;
• излучение одних участков волнового фронта не оказывает влияния на другие;
• колебания излучаются в основном перпендикулярно поверхности волнового фронта;
• равные по площади участки волнового фронта излучают одинаковую интенсивность.

Дифракция на прямоугольной щели

В таком случае интерференционная картина выглядит как светлые и темные полосы. Наиболее яркая светлая полоса — главный максимум — находится в центре.

Преломление

Когда свет попадает из одной среды в другую, например, из воздуха в воду, он меняет направление, т.е. преломляется. Согласно принципу Гюйгенса-Френеля на границе сред из каждой точки исходит вторичное излучение.

Из принципа Гюйгенса можно получить, что показатель преломления равен отношению скоростей светового колебания в одной и другой среде. Также можно найти и угол, на который отклоняется свет.

Пятно Пуассона

Пятно Пуассона является доказательством того, что даже если вы правы, вы можете быть не правы. Узнайте, почему эта концепция физики привела к тому, что имя Симеона Пуассона прожило в позоре почти 200 лет.

В начале восемнадцатого столетия Французская академия решила провести товарищеский конкурс. Члены Академии, как и ученые всего мира, заметили, что когда свет перемещался из одной среды в другую, он изгибался. Стекло, вода, гель, все, что позволяет свету проходить через него, даст ему проход, только если он изменит свой ход. Люди могли измерить изгиб света, но были озадачены тем, что заставило это произойти. Французская академия пыталась решить эту проблему, противопоставляя умы разных ученых.

Помните Августина Френеля? Он был инженером и изучал эффекты света. Работая оттуда, он придумал новую идею; свет излучался волнами, перпендикулярными направлению, в котором он проходил. Его идея вызвала волнение, особенно у пуассоновских пэров. Они полагали, что свет путешествовал как ряд частиц, все из которых имели сложные взаимодействия друг с другом. Пуассон, Френель и другие ученые собрались вместе и провели волнующую серию дискуссий о природе света и наблюдаемых эффектах его путешествия через различные среды.

К концу дебатов Пуассон выдвинул аргумент, который, казалось, сжег теорию Френеля до основания и “засолил землю под ней”. Если кого-то забрасывают предметами, его лучший шанс избежать травмы – спрятаться за более крупным предметом (по крайней мере, пока ракеты, ищущие тепло, не разрушат его для всех). Спрячьтесь за скалой, и поток гальки отскочит от скалы и пролетит мимо, не задев вас. Если, с другой стороны, человек по пояс в воде и хочет спрятаться от волны, он не будет в безопасности, приседая за скалой. Волны огибают твердые предметы.

Пуассон рассуждал, что если свет действительно был волной, то когда свет включался на совершенно сферическом объекте, световые волны могли бы огибать этот объект. Идеальная симметрия сферы означала, что все световые волны встретятся в точном центре тени позади нее, ведь там люди смогут увидеть яркое пятно света.

Это было нелепо. После выступления, как все закончили смеяться,  успешные французские ученые пошли развлечься или выпить что-нибудь в близлежащем заведении. По крайней мере, один человек не присоединился к ним. Доминик Араго, один из судей, понял, что Пуассон описал идеальный эксперимент. Он нашел круглый предмет, он нашел свет, и довольно скоро он нашел это пятно. Что явилось подтверждением словам Пуассона.

Ничего не оставалось, кроме как вручить приз Френелю. Пуассон выдвинул следствие света как волны, которая была настолько нелепой, настолько маловероятной, что это не могло быть объяснено ничем другим. Френель был достаточно умен, чтобы выдвинуть теорию. Пуассон был достаточно умен, чтобы доказать, что Френель прав, и доказать, что он не прав. Несмотря на то, что Доминик Араго действительно прошел тест, крошечная точка света в центре тени сферического объекта всегда называлась Пятном Пуассона. В физике нет вечного движения, но есть постоянные насмешки.

Ослабление сигнала за счет препятствий. Зоны Френеля

Для объяснения явления огибания радиоволнами различных препятствий, их проникновения в области тени и полутени используется принцип Гюйгенса – Френеля. В соответствии с моделью Френеля область распространения радиоволн между передающим и приемным устройствами ограничивается эллипсоидом вращения вокруг линии, их соединяющей. Этот эллипсоид многослойный и может включать в себя бесконечно много зон.

Ближайшая к линии, соединяющей передатчик с приемником, зона называется первой зоной Френеля. На рис. 3 представлено продольное сечение первой зоны Френеля.

Принято считать, что существенной при распространении радиоволн является первая зона Френеля (примерно половина передаваемой энергии). Без учета потерь сигнала в данной зоне расчет радиолинии невозможен.

Для любой точки радиолинии радиус первой зоны Френеля (R0) можно найти по формуле:

R0= (λ (Lтр – rтек ) r тек / Lтр )1/2,                     (4)

где λ – длина волны (м), Lтр – расстояние между передатчиком и приемником (м), rтек – удаление от источника сигнала (м). Наибольший радиус для первой зоны Френеля определяется по формуле:

Rn = 0,5 (λLтр)1/2.                                            (5)

Если бы сигнал не встречал препятствий во всей первой зоне Френеля, можно было бы ограничиться только учетом ослабления сигнала в свободном пространстве. Но такое бывает очень редко. В зависимости от наличия преград радиолинии делятся на открытые, полуоткрытые и закрытые.

На рис. 4 изображено 2 типа препятствий. Если в первой зоне Френеля имеется препятствие, не пересекающее линию прямой видимости (hпреп.1), то такой радиоинтервал называется полуоткрытым, в противном случае (hпреп.2) – закрытым. Причем нужно учитывать перекрытие зоны Френеля как в вертикальной (рис. 4), так и в горизонтальной плоскости.

Отношение значения просвета hпреп.1 или hпреп.2 к радиусу зоны Френеля R1 или R2 называется относительным просветом:

p(0) = hпреп. i / Ri.                                                 (6)

Для полуоткрытого интервала p(0) имеет положительное значение, для закрытого – отрицательное. При совпадении наивысшей точки препятствия с линией прямой видимости p(0) = 0.

В соответствии со значением p(0) и характером профиля препятствия можно по диаграмме (рис. 5) получить ослабление сигнала, вызванного наличием одиночного препятствия. При наличии двух и более препятствий в случае их близкого расположения они заменяются одним эквивалентным. Если расстояние между препятствиями превышает сумму длин самих препятствий, то ослабление сигнала считается раздельно для каждого из них.

Как видно из диаграммы, наибольшее ослабление вносит препятствие с плоской или гладкой сферической поверхностью. Закрытие плоским рельефом нижней части зоны Френеля более чем на 75% ведет к ослаблению сигнала более чем на 15–20 дБ.

При дальности радиолинии более 5 км необходимо дополнительно как препятствие учитывать кривизну Земли:

Hмакс = 1,96 . 10-2 • Lтр2                                  (7),

где Hмакс – максимальная высота препятствия, создаваемая за счет кривизны Земли (м), Lтр – расстояние между передатчиком и приемником (км).

Значения высоты препятствия, создаваемого за счет кривизны Земли, для относительных расстояний rтек / Lтр приведены в таблице.

Зоны Френеля для плоской волны

Рассмотрим разбивку площади отверстия на более тонкие кольца с равной площадью. Эти круги являются вторичными источниками света. Амплитуда световой волны, пришедшей от каждого кольца к наблюдателю, примерно одинакова. Кроме того, разность фаз от соседнего круга в точке Н также одинакова. В таком случае комплексные амплитуды в точке наблюдателя при сложении на единой комплексной плоскости образуют часть окружности – дугу. Суммарная же амплитуда – это хорда. Теперь рассмотрим, каким образом меняется картина суммирования комплексных амплитуд в случае изменения радиуса отверстия при условии сохранения остальных параметров задачи. В том случае, если отверстие открывает для наблюдателя всего одну зону, картина сложения будет представлена частью окружности. Амплитуда от последнего кольца будет повернута на угол π относительно центральной части, т. к. разность хода первой зоны, согласно определению, равна λ/2. Данный угол π будет означать, что амплитуды составят половину окружности. В таком случае сумма этих значений в точке наблюдения будет равна нулю – нулевая длина хорды. Если будет открыто три кольца, то картина представит собой полторы окружности и так далее. Амплитуда в точке наблюдателя для четного количества колец равна нулю. А в случае когда используют нечетное число кругов, она будет максимальной и равной значению длины диаметра на комплексной плоскости сложения амплитуд. Рассмотренные задачи в полной мере раскрывают метод зон Френеля.

Принцип Гюйгенса

Работу подобного явления описал Христиан Гюйгенс. После определённого количества проведённых экспериментов со световыми волнами на водной поверхности, он предложил науке новое объяснение такого феномена и дал ему название «волновой фронт». Таким образом, Христиан дал возможность понять, как будет вести себя луч света при попадании на какую-то поверхность другого типа.

Его принцип звучит следующим образом:

Точки поверхности, заметные в определённый момент времени, могут быть причиной для вторичных элементов. Площадь, которая прикасается ко всем вторичным волнам, считается волновой сферой в последующие отрезки времени.

Он объяснил, что все элементы следует рассматривать как начало сферических волн, которые имеют название как вторичные волны. Христиан заметил, что волновой фронт по своей сути является совокупностью этих точек касания, отсюда и выплывает весь его принцип. Кроме этого, вторичные элементы представляются сферической формы.

Стоит запомнить, что волновой фронт — это точки геометрического смысла, до которых доходят колебания к определённому моменту времени.

Вторичные элементы Гюйгенса представляются не как настоящие волны, а лишь дополнительные, имеющие форму сферы, используемые не для расчёта, а лишь приблизительного построения. Поэтому эти сферы вторичных элементов по своей сути имеют только огибающее действие, что позволяет образовываться новому волновому фронту. Этот принцип хорошо объясняет работу дифракции света, однако решает вопрос только направления фронта, а не объясняет, откуда появляется амплитуда, интенсивность волн, распыление волн и их обратное действие. Френель использовал принцип Гюйгенса для устранения этих недостатков и дополнения его работы физическим смыслом. Через некоторое время учёный представил свою работу, которая полностью подержалась научным сообществом.

19.3. Зоны Френеля

Вычисление интеграла в пункте ()
в общем случае — трудная задача.

В случаях, если в задаче существует симметрия, амплитуду
результирующего колебания можно найти методом зон Френеля, не прибегая к вычислению
интеграла.

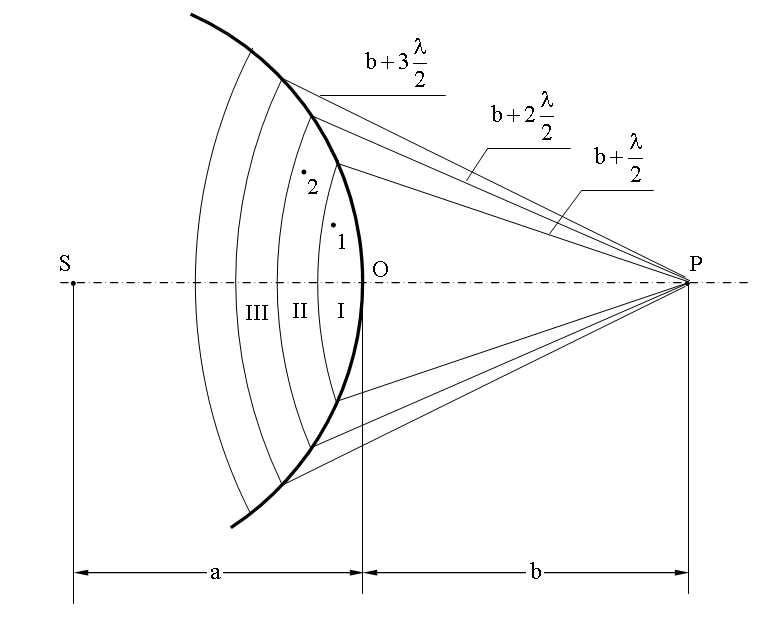
Пусть от источника света S распространяется
монохроматическая сферическая волна, P — точка
наблюдения. Через точку O проходит сферическая
волновая поверхность. Она симметрична относительно прямой SP.
Разобьем эту поверхность на кольцевые зоны I, II, III
и т.д. так, чтобы расстояния от краев зоны до точки P
отличались на λ/2 — половину длины световой
волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Что дает такое разбиение для расчета интенсивности в точке
P? Возьмем произвольную точку 1 в первой зоне
Френеля. В зоне II найдется, в силу правила построения
зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку
P от точек 1 и 2 будет равна λ/2.
Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

Из геометрических соображениях следует, что при не очень
больших номерах зон их площади примерно одинаковы. Значит каждой точке первой
зоны найдется соответствующая ей точка во второй, колебания которых погасят
друг друга. Амплитуда результирующего колебания, приходящего в точку P
от зоны с номером m, уменьшается с ростом m,
т.е.

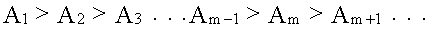
Происходит это из-за увеличения с ростом m
угла между нормалью к волновой поверхности и направлением на точку P.
Значит гашение колебаний соседних зон будет не совсем полным.

Пусть на пути сферической световой волны, испускаемой источником
S, расположен непрозрачный экран с круглым отверстием
радиуса r. Если отверстие
открывает четное число зон Френеля, то в точке P
будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние
пары, колебания которых в точке P приблизительно
гасят друг друга.

При нечетном числе зон в точке P
будет максимум, так как колебания одной зоны останутся не погашенными.

Можно показать, что радиус зоны Френеля с номером m при не
очень больших m:

.

Расстояние «a» примерно
равно расстоянию от источника до преграды, расстояние «b»
— от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля,
то, приравняв r и
r_m, получим формулу
для подсчета числа открытых зон Френеля:

.

При m четном в точке P
будет минимум интенсивности, при нечетном — максимум.

В случае дифракции Фраунгофера параметр b2/(Lλ
) << 1 ().
Это значит, что если размер препятствия b ~ λ,
то расстояние до экрана наблюдения L >> b.

Пусть на длинную щель шириной b
падает плоская монохроматическая волна с длиной λ.

Поместим между щелью и экраном наблюдения линзу так, чтобы
экран наблюдателя находился в фокальной плоскости линзы. Линза позволяет наблюдать
на экране дифракцию в параллельных лучах (L → ∞
).

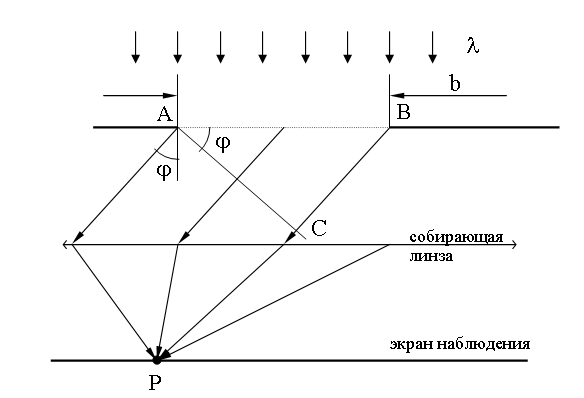
Собирающая линза обладает свойством, называемым таутохронностью:
лучи, идущие от волновой поверхности AC до точки
наблюдения P имеют одинаковую оптическую длину.
Таким образом результат суперпозиции вторичных волн, который определяет амплитуду
колебаний световой волны в точке P (см.), зависит от разности хода, набегающей в треугольнике ABC.

Для нахождения положений максимумов и минимумов интенсивности
воспользуемся методом зон Френеля ():
разобьем сторону BC на отрезки длиной λ/2.

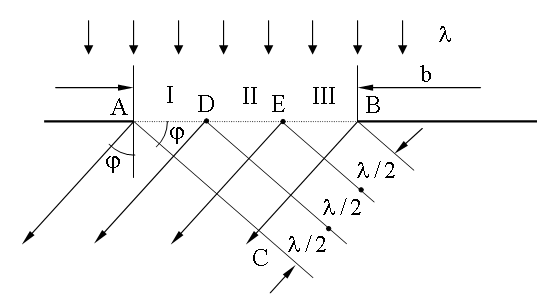
Из концов этих отрезков проведем линии, параллельные фронту
вторичной плоской волны, идущей под углом φ.
Эти линии разобьют AB — фронт первичной плоской
волны на зоны Френеля. На рисунке их изображено три: AD,
DE и EB. Число зон Френеля k
зависит от λ и длины отрезка BC = b
Sinφ . Если k целое, то

.

При четном числе зон Френеля k = 2m,
где m = ±1, ±2… все зоны можно
разбить на соседние пары, которые гасят друг друга ().
Следовательно условие минимума при дифракции Фраунгофера на щели имеет вид:

При нечетном k = 2m + 1
одна зона остается без пары и ее колебания не будут погашены, следовательно,
условие максимума при дифракции Фраунгофера на щели будет иметь вид:

.

Обратим внимание, что условия формально противоположны условиям
максимумов и минимумов ()
при интерференции от двух источников

Задача по определению размеров колец

Для начала следует представить, что поверхность плоского отверстия находится между источником света (точка С) и наблюдателем (точка Н). Она располагается перпендикулярно линии СН. Отрезок СН проходит через центр круглого отверстия (точка О). Так как наша задача имеет ось симметрии, то зоны Френеля будут иметь вид колец. А решение будет сводиться к определению радиуса этих кругов с произвольным номером (м). При этом максимальное значение называют радиусом зоны. Для решения задачи необходимо сделать дополнительное построение, а именно: выбрать произвольную точку (А) в плоскости отверстия и соединить ее отрезками прямых линий с точкой наблюдения и с источником света. В результате получаем треугольник САН. Далее можно сделать так, что световая волна, приходящая к наблюдателю по пути САН, пройдет больший путь, чем та, которая пойдет по пути СН. Отсюда получаем, что разность хода СА+АН-СН определяет разность волновых фаз, которые прошли от вторичных источников (А и О) в точку наблюдения. От этого значения зависит результирующая интерференция волн с позиции наблюдателя, а следовательно и световая интенсивность в этой точке.

Историческая справка

Огюстен Жан Френель (10.06.1788–14.07.1827) – французский физик. Посвятил свою жизнь изучению свойств физической оптики. Он еще в 1811 году под влиянием Э. Малюса начал самостоятельно изучать физику, вскоре увлекся экспериментальными исследованиями в области оптики. В 1814 году «переоткрыл» принцип интерференции, а в 1816-м дополнил широко известный принцип Гюйгенса, в который ввел представление о когерентности и интерференции элементарных волн. В 1818 г., опираясь на проделанную работу, разработал теорию дифракции света. Он ввел практику рассмотрения дифракции от края, а также от круглого отверстия. Проводил опыты, ставшие впоследствии классическими, с бипризмами и бизеркалами по интерференции света. В 1821 г. доказал факт поперечности световых волн, в 1823-м открыл круговую и эллиптическую поляризации света. Объяснил на основе волновых представлений хроматическую поляризацию, а также вращение плоскости поляризации света и двойное лучепреломление. В 1823 г. установил законы преломления и отражения света на неподвижной плоской поверхности раздела двух сред. Наряду с Юнгом считается создателем волновой оптики. Является изобретателем ряда интерференционных приборов, таких как зеркала Френеля или бипризма Френеля. Считается основателем принципиально нового способа маячного освещения.