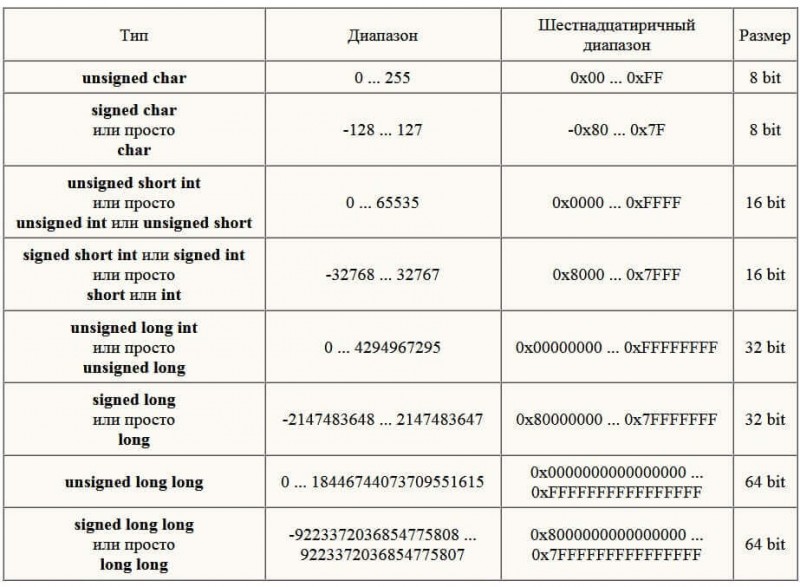
Урок №39. арифметические операторы

Проблемы чисел с плавающей точкой

Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль. Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.

Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.

a = 0.1
for i in range(13):
    a += 0.1
print(a)

1.4000000000000001

Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.

Примечания

1. Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
2. ISO/IEC 9899:TC2: When integers are divided, the result of the operator is the algebraic quotient with any fractional part discarded. ; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится.
3. ISO/IEC 14882:2003 : Programming languages — C++, 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
4. N3242=11-0012 (Working draft), текст совпадает с C99
5.  (англ.). dlang.org. Дата обращения 29 октября 2017.
6. К. Арнолд, Дж. Гослинг, Д. Холмс. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
7. Стандарт 1973 года: div — division with truncation.

Простые примеры

Оператор, действующий над пространствами функций — это правило, согласно которому одна функция преобразуется в другую. Преобразование функции x(t){\displaystyle x(t)} согласно правилу A{\displaystyle A} в другую функцию y(t){\displaystyle y(t)} имеет вид y(t)=A{x(t)}{\displaystyle y(t)=A\{x(t)\}} или, проще, y=Ax{\displaystyle y=Ax}.

Примеры подобных преобразований — умножение на число: y(t)=cx(t){\displaystyle y(t)=cx(t)} и дифференцирование: y(t)=dx(t)dt{\displaystyle \scriptstyle y(t)={\frac {dx(t)}{dt}}}. Соответствующие операторы называются операторами умножения на число, дифференцирования, интегрирования, решения дифференциального уравнения и т. д.

Операторы, изменяющие аргумент функции, называются операторами преобразования или преобразованиями. Преобразование подменяет координатные оси, отображает функцию в другое пространство. Например преобразование Фурье из временной в частотную область:

F(ω)=12π∫−∞∞f(t)e−itωdt=F{f(t)}.{\displaystyle F(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(t)e^{-it\omega }\,dt={\mathcal {F}}\{f(t)\}.}

Отличие оператора от простой суперпозиции функций в данном случае заключается в том, что значение функции y{\displaystyle y}, вообще говоря, в каждой точке t{\displaystyle t} зависит не только от x(t){\displaystyle x(t)}, а от значений функции x{\displaystyle x} во всех точках t{\displaystyle t}. Поясним на примере преобразования Фурье. Значение этого преобразования (спектр функции) в точке ω{\displaystyle \omega } меняется при непрерывном изменении исходной функции в окрестности любой точки t{\displaystyle t}.

Изучением общих свойств операторов и применением их к решению различных задач занимается теория операторов. Например, оказывается, что у оператора умножения вектора на матрицу и оператора свёртки функции с весом есть много общих свойств.

Фундаментальным для практики является класс так называемых линейных операторов. Он также является наиболее исследованным. В качестве примера линейного оператора можно привести операцию умножения n{\displaystyle n}-мерного вектора на матрицу размером n×m{\displaystyle n\times m}. Этот оператор отображает n{\displaystyle n}-мерное пространство векторов в m{\displaystyle m}-мерное.

Свойства

Далее описаны основные свойства операция умножения на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} }.

Умножение коммутативно, то есть от перемены мест сомножителей произведение не меняется. Свойство также известно как переместительный закон умножения:

Коммутативность: a⋅b=b⋅a;{\displaystyle a\cdot b=b\cdot a;}

Умножение ассоциативно, то есть при последовательном выполнении умножения трёх или более чисел последовательность выполнения операций не имеет значения. Свойство также известно как сочетательный закон умножения:

Ассоциативность: (a⋅b)⋅c=a⋅(b⋅c);{\displaystyle (a\cdot b)\cdot c=a\cdot (b\cdot c);}

Умножение дистрибутивно, это свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Свойство также известно как распределительный закон:

Дистрибутивность: x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A;{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A;}

Относительно умножения в множестве A{\displaystyle A} существует единственный нейтральный элемент — 1{\displaystyle 1} (число «один»). Умножение любого числа на 1{\displaystyle 1} (нейтральный элемент) даёт число, равное исходному:

Нейтральный элемент: x⋅1=1⋅x=x,∃!1∈A;{\displaystyle x\cdot 1=1\cdot x=x,\quad \exists !1\in A;}

Умножение на 1{\displaystyle 1} идемпотентно, то есть повторное применение операции к объекту даёт тот же результат, что и одинарное:

Идемпотентность: x=x⋅1=(x⋅1)⋅1=((x⋅1)⋅1)⋅…⋅1,∀x∈A,∃!1∈A;{\displaystyle x=x\cdot 1=(x\cdot 1)\cdot 1=((x\cdot 1)\cdot 1)\cdot …\cdot 1,\quad \forall x\in A,\quad \exists !1\in A;}

Умножение на 0{\displaystyle 0} (нулевой элемент) даёт 0{\displaystyle 0} (нуль):

Нулевой элемент: x⋅=⋅x=,∃!∈A.{\displaystyle x\cdot 0=0\cdot x=0,\quad \exists !0\in A.}

Операция умножения чисел, определённых на множествах N,Z,Q,R{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} }, даёт произведение, принадлежащее этому же множеству. Следовательно, операция умножения относится к замкнутым операциям, то есть множества чисел Z,Q,R{\displaystyle \mathbb {Z} ,\mathbb {Q} ,\mathbb {R} } образуют кольца относительно операции умножения.

На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что Z−,Q−,R−{\displaystyle \mathbb {Z} _{-0},\mathbb {Q} _{-0},\mathbb {R} _{-0}} являются абелевыми группами относительно операции умножения.

В математических выражениях операция умножения имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.

На множестве вещественных чисел область значений функции умножения графически имеет вид поверхности проходящей через начало координат и изогнутой с двух сторон в виде параболы.

Тест

Задание №1

Вычислите результат следующего выражения: .

Ответ №1

Поскольку операторы и имеют более высокий приоритет, чем оператор , то оператор  будет выполняться последним. Мы можем переписать наше выражение следующим образом: . Операторы и имеют одинаковый приоритет, но их ассоциативность слева направо, так что левый оператор будет выполняться первым. Получается: .

Ответ: 8.

Задание №2

Напишите программу, которая просит пользователя ввести целое число, а затем сообщает, является ли его число чётным или нечётным. Напишите функцию isEven(), которая возвращает , если целое число является чётным. Используйте оператор деления с остатком, чтобы определить чётность числа.

Подсказка: Используйте ветвление if и оператор сравнения ().

Ответ №2

#include <iostream>

bool isEven(int x)
{
// Если x % 2 == 0, то x — это чётное число
return (x % 2) == 0;
}

int main()
{
std::cout << «Enter an integer: «;
int x;
std::cin >> x;

if (isEven(x))
std::cout << x << » is even\n»;
else
std::cout << x << » is odd\n»;

return 0;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

#include <iostream> boolisEven(intx) { // Если x % 2 == 0, то x — это чётное число return(x%2)==; } intmain() { std::cout<<«Enter an integer: «; intx; std::cin>>x; if(isEven(x)) std::cout<<x<<» is even\n»; else std::cout<<x<<» is odd\n»; return; }

Примечание: Возможно, вы хотели написать или написали функцию isEven() следующим образом:

bool isEven(int x)
{
if ((x % 2) == 0)
return true;
else
return false;
}

1 2 3 4 5 6 7

boolisEven(intx) { if((x%2)==) returntrue; else returnfalse; }

Хотя этот способ тоже рабочий, но он сложнее. Посмотрим, как его можно упростить. Во-первых, давайте вытащим условие if и присвоим его отдельной переменной типа bool:

bool isEven(int x)
{
bool isEven = (x % 2) == 0;
if (isEven) // isEven — true
return true;
else // isEven — false
return false;
}

1 2 3 4 5 6 7 8

boolisEven(intx) { boolisEven=(x%2)==; if(isEven)// isEven — true returntrue; else// isEven — false returnfalse; }

В коде, приведенном выше, если переменная имеет значение , то возвращаем , в противном случае (если имеет значение ) — возвращаем . Мы же можем сразу возвращать :

bool isEven(int x)
{
bool isEven = (x % 2) == 0;
return isEven;
}

1 2 3 4 5

boolisEven(intx) { boolisEven=(x%2)==; returnisEven; }

Так как переменная используется только один раз, то мы можем её вообще исключить:

bool isEven(int x)
{
return (x % 2) == 0;
}

1 2 3 4

boolisEven(intx) { return(x%2)==; }

Принцип работы[править]

Умножение в бинарной системеправить

Умножение в столбик

Умножение в бинарной системе счисления происходит точно так же, как в десятичной — по схеме умножения столбиком.
Если множимое — разрядное, а множитель — разрядный, то для формирования произведения требуется вычислить частичных произведений и сложить их между собой.

Вычисление частичных произведенийправить

В бинарной системе для вычисления частичного произведения можно воспользоваться логическими элементами — конъюнкторами.
Каждое частичное произведение — это результат выполнения логических операции ( между текущим , где , разрядом множителя и всеми разрядами множимого) и сдвига результата логической операции влево на число разрядов, соответствующее весу текущего разряда множителя. Матричный умножитель вычисляет частичные произведения по формуле:

Суммирование частичных произведенийправить

На этом этапе происходит сложение всех частичных произведений .

Схемаправить

Схема матричного умножителя

Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик для двух четырёх — разрядных чисел приведена на рисунке.
Формирование частичных произведений осуществляется посредством логических элементов .
Полные одноразрядные сумматоры обеспечивают формирование разрядов результата.
Разрядность результата — определяется разрядностью множителя — и множимого — :

.

Все конъюнкторы работают параллельно.
Полные одноразрядные сумматоры обеспечивают поразрядное сложение результатов конъюнкций и переносов из предыдущих разрядов сумматора.
В приведенной схеме использованы четырех разрядные сумматоры с последовательным переносом.
Время выполнения операции умножения определяется временем распространения переносов до выходного разряда .

Если внимательно посмотреть на схему матричного умножителя (англ. binary multiplier), то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа и числа . В точках пересечения этих проводников находятся логические элементы . Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.

Умножение последовательностей

Произведение элементов последовательности может быть компактно записано с помощью специального символа умножения, восходящего к заглавной букве Π (пи) греческого алфавита, как показано в примере:

∏i=14i=1⋅2⋅3⋅4=24.{\displaystyle \prod _{i=1}^{4}i=1\cdot 2\cdot 3\cdot 4=24.}

Снизу записывается символ свободной переменной (в данном случае i{\displaystyle i}), называемой «индексом умножения», вместе с начальным значением (в данном случае 1). Сверху записывается конечное значение (в данном случае 4) в виде числа или переменной, либо символ бесконечности ∞{\displaystyle \infty }, если предполагается бесконечное произведение. Такую запись можно «развернуть» в выражение, в котором последовательно подставляются значения индекса умножения от начального до конечного значения:

∏i=mnxi=xm⋅xm+1⋅xm+2⋅⋯⋅xn−1⋅xn,{\displaystyle \prod _{i=m}^{n}x_{i}=x_{m}\cdot x_{m+1}\cdot x_{m+2}\cdot \,\,\cdots \,\,\cdot x_{n-1}\cdot x_{n},}

где m и n есть целые числа или выражения, которые вычисляются в целочисленные значения.

Если значения индекса заданы некоторым множеством, то многократное произведение может быть записано с его помощью, например

∏i∈Axi{\displaystyle \prod _{i\in A}x_{i}}.

Такая запись означает, что переменная i{\displaystyle i} «пробегает» все значения, принадлежащие множеству A{\displaystyle A}.

Умножение физических величин

См. также: Единицы физических величин

Единица измерения физической величины имеет определенное наименование (размерность), например, для длины — метр (м), для времени — секунда (с), для массы — грамм (г) и так далее. Результат измерения той или иной величины представляет собой не просто число, а число с размерностью, например, 10 м, 145 с, 500 г. Размерность представляет собой самостоятельный объект, который равноправно участвует в операции умножения. При умножении физических величин умножаются как сами числовые значения, так и их размерности, порождая новое число с новой размерностью. Например, прямоугольник со сторонами 5 м и 3 м обладает площадью, получаемой умножением длин сторон:

5 м · 3 м = 5 · 3 м·м= 15 м·м, или 15 м².

Таким образом, умножение физических величин надо рассматривать как нахождение новой физической величины, отличающейся от величин, которые мы умножаем. Если физически возможно создание такого произведения, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин  присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее.

Например, если умножить скорость равномерно и прямолинейно движущегося тела, равную 5 м/с, на время, равное 3 с, то получится именованное число (физическая величина), которая называется «длина», или «расстояние» и измеряется в метрах:

5 м/с · 3 с = 15 (м/с) · с = 15 м.

Помимо размерных физических величин существуют безразмерные величины. Безразмерные величины либо просто определяют некоторое количество (измеряются «штуками», «разами» и тому подобное), либо являются отношениями физических величин одной и той же размерности, например, относительная плотность является отношением плотности тела к эталонной плотности (обычно, плотности воды). При умножении величины с размерностью на безразмерную величину результат сохраняет исходную размерность. Например, если взять 5-метровые рейки в количестве 3 штуки, то в результате умножения получим общую длину реек 15 метров:

5 м · 3 = 15 м.

Количество реек (безразмерная величина) здесь не зависит ни от способа их подсчёта, ни от единицы измерения их длины. Например, если измерить длину не в метрах, а в футах, то длина той же рейки составит 16,4 фута, а общая длина трёх реек:

16,4 фута · 3 = 49,2 фута.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Нарезка строк

Одной из тем, которую вы часто будете делать на практике, является нарезка строк. Помню, меня удивило то, как часто мне нужно было узнать, как это делается в повседневной работе. Давайте посмотрим, как нарезка сработает в следующей строке:

Python

my_string = «I like Python!»

1	my_string=»I like Python!»

Каждый символ в строке может стать доступным при помощи слайсинга (нарезки). Например, если вам нужно взять только первый символ, вы можете сделать это следующим образом:

Python

print( my_string ) # I

1	print(my_string1)# I

Таким образом, мы берем первый символ в строке до второго символа, но, не включая его. Да, в Python отсчет ведется с нуля. Это проще понять, если мы определим позицию каждого символа в таблице:

Python

0 1 2 3 4 5 6 7 8 9 10 11 12 13 — I l i k e P y t h o n !

1	12345678910111213-IlikePython!

Таким образом, у нас есть строка длиной в 14 символов, начиная с нуля и до тринадцати. Давайте приведем несколько примеров, чтобы понять это лучше.

Python

my_string # ‘I’
my_string # ‘I like Pytho’
my_string # ‘I like Python’
my_string # ‘I like Python!’
my_string # ‘I like Py’
my_string # ‘I like Python!’
my_string # ‘like Python!’

1 2 3 4 5 6 7

my_string1# ‘I’ my_string12# ‘I like Pytho’ my_string13# ‘I like Python’ my_string14# ‘I like Python!’ my_string-5# ‘I like Py’ my_string# ‘I like Python!’ my_string2# ‘like Python!’

Как видно в данных примерах, мы можем назначить срез, лишь указав его начало (другими словами, my_string), конец среза (my_string), или оба (my_string). Мы можем даже использовать отрицательные значения, которые начинаются с конца строки. Так что в примере, где мы указали my_string, начало ведется с нуля и заканчивается 5 символами, перед концом строки. Вы можете задаться вопросом «Зачем мне это и где это можно применить?». Лично я использовал это для разбора записей с фиксированной шириной в файлах, или ситуативно для парсинга сложных названий файлов, с очень специфическими наименованиями. Также я использовал это для парсинга значений в бинарных файлах. Любая работа, которая включает в себя обработку текстовых файлов, может быть намного проще, если вы понимаете, как работает нарезка и как эффективно использовать данный инструмент. Вы также можете получить доступ к отдельным символам в строке с помощью индексации. Например:

Python

print(my_string) # I

1	print(my_string)# I

Данный код выдаст первый символ в строке.

Деление (/)

Сложение, вычитание и умножение тривиальны, а вот с делением не всё так просто. В Python существует три вида деления и столько же разных операторов. Начнём с истинного деления, за которое отвечает оператор «». Его главным отличием является то, что, вне зависимости от типов операндов, будет возвращен вещественный результат ().

Этот вид деления наиболее близок к обычному и знакомому нам математическому. И здесь тоже нельзя делить на ноль:

Немного истории. В старых версиях Питон оператор «/» выполнял операцию классического деления: т.е. он делил целочисленно и усекал дробную часть в том случае, когда делимое и делитель были целыми. Если же операнды принадлежали к множеству вещественных чисел, то проводилось деление с сохранением дробной части, и результат был float.

Разработчики отказались от классического деления в Python 3.0 и вместо него добавили истинное деление. Архитекторы языка пошли на такой шаг по той причине, что в предыдущей модели классического деления результаты напрямую зависели от типов операндов. Из-за этого возникали трудности с их предварительной идентификацией и оценкой, что было особенно критично для Питона, как для языка с динамической типизацией.

Примечания

1. ↑ Умножение //  :  / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
2. ↑ Так это свойство обычно называется в школьных учебниках
3. , с. 165.
4. .
5. , с. 20.
6. Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида {xα<x<β}{\displaystyle \{x:\alpha <x<\beta \}}
7. , с. 46.
8. Волинская Н. И. . brestschool7.iatp.by. Дата обращения 18 апреля 2016.
9. Макаров Владимир Петрович. . lithology.ru, Литология.РФ. Дата обращения 18 апреля 2016.

Где оператор возведения в степень?

В C++ вместо оператора возведения в степень есть функция pow(), которая находится в заголовочном файле cmath. эквивалентно . Стоит отметить, что параметры pow() имеют тип double, поэтому вы можете использовать не только целые числа, но и дробные. Например:

#include <iostream>
#include <cmath> // подключаем pow()

int main()
{
std::cout << «Enter the base: «;
double base;
std::cin >> base;

std::cout << «Enter the exponent: «;
double exp;
std::cin >> exp;

std::cout << base << «^» << exp << » = » << pow(base, exp) << «\n»;

return 0;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

#include <iostream> #include <cmath> // подключаем pow() intmain() { std::cout<<«Enter the base: «; doublebase; std::cin>>base; std::cout<<«Enter the exponent: «; doubleexp; std::cin>>exp; std::cout<<base<<«^»<<exp<<» = «<<pow(base,exp)<<«\n»; return; }

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Операции над битовыми векторами

Битовые сдвиги

К битовым операциям также относят битовые сдвиги. При сдвиге значения битов копируются в соседние по направлению сдвига. Различают несколько видов сдвигов — логический, арифметический и циклический, в зависимости от обработки крайних битов.

Также различают сдвиг влево (в направлении от младшего бита к старшему) и вправо (в направлении от старшего бита к младшему).

Файл:Rotate right logically.svg

Логический сдвиг

Файл:Rotate right arithmetically.svg

Арифметический сдвиг (правый)

Файл:Rotate right.svg

Циклический сдвиг

Файл:Rotate right through carry.svg

Циклический сдвиг через перенос

Логический сдвиг

При логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение.

Логические сдвиги влево и вправо используются для быстрого умножения и деления на 2, соответственно.

Арифметический сдвиг

Арифметический сдвиг аналогичен логическому, но значение слова считается знаковым числом представленному дополнительным кодом. Так при правом сдвиге старший бит сохраняет свое значение. Левый арифметический сдвиг идентичен логическому.

Циклический сдвиг

При циклическом сдвиге, значение последнего бита по направлению сдвига копируется в первый бит (и копируется в бит переноса).

Также различают циклический сдвиг через бит переноса — при нем первый бит по направлению сдвига получает значение из бита переноса, а значение последнего бита сдвигается в бит переноса.

Линейные операторы

Основная статья: Линейное отображение

Оператор L{\displaystyle L} (действующий из векторного пространства в векторное же) называется линейным однородным (или просто линейным), если он обладает следующими свойствами:

1. может применяться почленно к сумме аргументов:

   L(x1+x2)=L(x1)+L(x2){\displaystyle L(x_{1}+x_{2})=L(x_{1})+L(x_{2})};

2. скаляр (постоянную величину) c{\displaystyle c} можно выносить за знак оператора:

   L(cx)=cL(x){\displaystyle L(cx)=cL(x)};

Из второго свойства следует, что для линейного однородного оператора справедливо свойство L()={\displaystyle L(0)=0}.

Оператор L{\displaystyle L} называется линейным неоднородным, если он состоит из линейного однородного оператора с прибавлением некоторого фиксированного элемента:

L{x}=L{x}+φ{\displaystyle L\{x\}=L_{0}\{x\}+\varphi },

где L{\displaystyle L_{0}} — линейный однородный оператор.

В случае линейного преобразования дискретных функций (последовательностей, векторов) новые значения функций yk{\displaystyle y_{k}} являются линейными функциями от старых значений xk{\displaystyle x_{k}}:

yk=∑l=1nTklxl{\displaystyle y_{k}=\sum _{l=1}^{n}T_{kl}\,x_{l}}.

В более общем случае непрерывных функций двумерная матрица весов принимает вид функции двух переменных K(t,ω){\displaystyle K(t,\;\omega )}, и называется ядром линейного интегрального преобразования:

φ(t)=∫VK(t,ω)f(ω)dω=K{f(ω)}.{\displaystyle \varphi (t)=\int \limits _{V}\!K(t,\omega )f(\omega )\,d\omega =K\{f(\omega )\}.}

Функция-операнд f(ω){\displaystyle f(\omega )} в данном случае называется спектральной функцией. Спектр может быть и дискретным, тогда f(ω){\displaystyle f(\omega )} заменяется вектором W{\displaystyle W}. В этом случае φ(t){\displaystyle \varphi (t)} представимо конечным или бесконечным рядом функций:

φ(t)=∑i=1nTi(t)wi.{\displaystyle \varphi (t)=\sum _{i=1}^{n}T_{i}(t)w_{i}.}

Переменные в C++

Теперь попробуем создать свои переменные.

Для начала объявим переменную, то есть скажем компьютеру, что нам нужно занять место в памяти. Для этого укажем тип данных, а потом название переменной.

Код	Как читается
int x;	Объявить целочисленную переменную x без значения.

Так создаётся переменная без значения. Если вы хотите, чтобы в ней сразу было какое-то число, то нужно использовать знак присваивания (=):

Код	Как читается
int y = 5;	Объявить целочисленную переменную y со значением 5.

Теперь в любое время можно менять значения переменных:

Код	Как читается
x = 6;	Присвоить переменной x значение 6.

Математический знак равенства (=) в программировании называется знаком присваивания.

Важно! Указывать тип данных нужно только при объявлении переменной. Давайте попробуем вывести значение какой-нибудь переменной на экран

Для этого напишем следующий код:

Давайте попробуем вывести значение какой-нибудь переменной на экран. Для этого напишем следующий код:

Внимательно прочтите этот код, а потом скомпилируйте и запустите программу:

Оператор декремента —Decrement operator —

Унарный оператор декремента уменьшает операнд на 1.The unary decrement operator decrements its operand by 1. Операндом должна быть переменная, свойство или индексатор.The operand must be a variable, a property access, or an indexer access.

Оператор декремента поддерживается в двух формах: постфиксный оператор декремента () и префиксный оператор декремента ().The decrement operator is supported in two forms: the postfix decrement operator, , and the prefix decrement operator, .

Постфиксный оператор уменьшенияPostfix decrement operator

Результатом является значение перед выполнением операции, как показано в следующем примере:The result of is the value of before the operation, as the following example shows:

Префиксный оператор декрементаPrefix decrement operator

Результатом является значение после выполнения операции, как показано в следующем примере:The result of is the value of after the operation, as the following example shows:

В программировании

Операция вычисления неполного частного и остатка в различных языках программирования

Язык	Неполноечастное	Остаток	Знак остатка
ActionScript			Делимое
Ada			Делитель
	Делимое
Бейсик			Не определено
Си (ISO 1990)		Не определено
Си (ISO 1999)		Делимое
C++ (ISO 2003)		Не определено
C++ (ISO 2011)		Делимое
C#		Делимое
ColdFusion			Делимое
Common Lisp			Делитель
		Делимое
D		Делимое
Delphi			Делимое
Eiffel			Делимое
Erlang			Делимое
Euphoria			Делимое
Microsoft Excel (англ.)			Делитель
Microsoft Excel (рус.)
FileMaker			Делитель
Fortran			Делимое
		Делитель
GML (Game Maker)			Делимое
Go		Делимое
Haskell			Делитель
		Делимое
J			Делитель
Java		Делимое
		Делитель (1.8+)
JavaScript	.toFixed(0)		Делимое
Lua			Делитель
Mathematica			Делитель
MATLAB			Делитель
		Делимое
MySQL			Делимое
Oberon			+, если делитель >0
Objective Caml			Не определено
Pascal			Делимое
Perl	Нет		Делитель
PHP	Нет		Делимое
PL/I			Делитель (ANSI PL/I)
Prolog (ISO 1995)			Делитель
PureBasic		Делимое
Python			Делитель
QBasic			Делимое
R			Делитель
RPG			Делимое
Ruby		Делитель
Scheme			Делитель
SenseTalk			Делитель
	Делимое
Tcl			Делитель
Verilog (2001)			Делимое
VHDL			Делитель
	Делимое
Visual Basic			Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция вычисляет остаток от деления, а операция осуществляет целочисленное деление, при котором остаток от деления отбрасывается:

78 mod 33 = 12
78 div 33 = 2

Знак остатка

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

• Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
• Знак остатка совпадает со знаком делителя: неполное частное округляет к −∞{\displaystyle -\infty }.

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

• Есть сумма n копеек, положительная или отрицательная. Перевести её в рубли и копейки: и . Знак остатка совпадает со знаком делимого.
• Есть бесконечное клеточное поле, каждая клетка 16×16 пикселей. В какую клетку попадает точка (x, y), и каковы координаты относительно верхнего левого угла клетки? Ответ: и соответственно. Знак остатка совпадает со знаком делителя.

Как запрограммировать, если такой операции нет?

Неполное частное можно вычислить через деление и взятие целой части: q=ab{\displaystyle q=\left}, где x{\displaystyle }, в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды остаток программируется как a−qb{\displaystyle a-qb}.

Если b{\displaystyle b} положительно, а знак r{\displaystyle r} совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой r′=(b+(amod⁡b))mod⁡b{\displaystyle r’=(b+(a\operatorname {mod} b))\operatorname {mod} b}.

Неполное частное и неотрицательный остаток от деления на степень двойки 2n{\displaystyle 2^{n}} — это битовый сдвиг a≫n{\displaystyle a\gg n} (для чисел со знаком — арифметический) и a&⁡(2n−1){\displaystyle a\mathop {\&} (2^{n}-1)}.