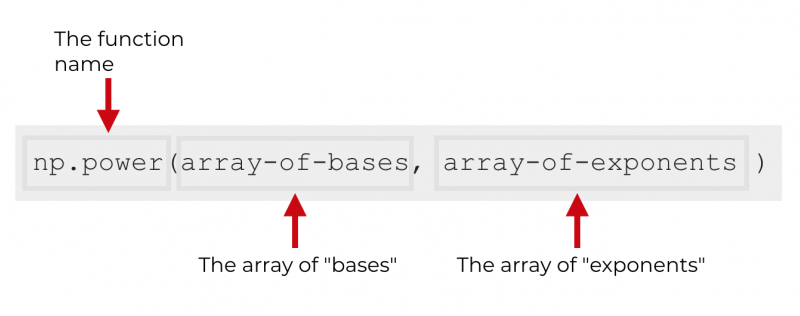
How to use numpy random normal in python

Содержание:

Introduction¶
- What’s New or Different
Numba¶
Оптимизация гиперпараметров. Раунд 1: RandomizedSearchCV
7.3. Статистика
Генерация случайного n-мерного массива целых чисел
Cython¶
Introduction¶
- What’s New or Different
Shuffling a String

Introduction¶

The new infrastructure takes a different approach to producing random numbers
from the object. Random number generation is separated into
two components, a bit generator and a random generator.

The has a limited set of responsibilities. It manages state
and provides functions to produce random doubles and random unsigned 32- and
64-bit values.

The takes the
bit generator-provided stream and transforms them into more useful
distributions, e.g., simulated normal random values. This structure allows
alternative bit generators to be used with little code duplication.

The is the user-facing object that is nearly identical to
. The canonical method to initialize a generator passes a
bit generator as the sole argument.

from numpy.random import default_rng
rg = default_rng(12345)
rg.random()

One can also instantiate directly with a instance.
To use the older algorithm, one can instantiate it directly
and pass it to .

from numpy.random import Generator, MT19937
rg = Generator(MT19937(12345))
rg.random()

What’s New or Different

Warning

The Box-Muller method used to produce NumPy’s normals is no longer available
in . It is not possible to reproduce the exact random
values using Generator for the normal distribution or any other
distribution that relies on the normal such as the or
. If you require bitwise backward compatible
streams, use .

The Generator’s normal, exponential and gamma functions use 256-step Ziggurat
methods which are 2-10 times faster than NumPy’s Box-Muller or inverse CDF
implementations.
Optional argument that accepts or
to produce either single or double prevision uniform random variables for
select distributions
Optional argument that allows existing arrays to be filled for
select distributions
All BitGenerators can produce doubles, uint64s and uint32s via CTypes
() and CFFI (). This allows the bit generators
to be used in numba.
The bit generators can be used in downstream projects via
.
is now the canonical way to generate integer
random numbers from a discrete uniform distribution. The and
methods are only available through the legacy .
The keyword can be used to specify open or closed intervals.
This replaces both and the deprecated .
is now the canonical way to generate floating-point
random numbers, which replaces ,
RandomState.sample, and RandomState.ranf. This is consistent with
Python’s .
All BitGenerators in numpy use to convert seeds into
initialized states.
The addition of an keyword argument to methods such as
, , and
improves support for sampling from and shuffling multi-dimensional arrays.

See for a complete list of improvements and
differences from the traditional .

Numba¶

Strings and character data in python

Numba can be used with either CTypes or CFFI. The current iteration of the
BitGenerators all export a small set of functions through both interfaces.

This example shows how numba can be used to produce gaussian samples using
a pure Python implementation which is then compiled. The random numbers are
provided by .

import numpy as np
import numba as nb

from numpy.random import PCG64
from timeit import timeit

bit_gen = PCG64()
next_d = bit_gen.cffi.next_double
state_addr = bit_gen.cffi.state_address

def normals(n, state):
    out = np.empty(n)
    for i in range((n + 1) // 2):
        x1 = 2.0 * next_d(state) - 1.0
        x2 = 2.0 * next_d(state) - 1.0
        r2 = x1 * x1 + x2 * x2
        while r2 >= 1.0 or r2 == 0.0
            x1 = 2.0 * next_d(state) - 1.0
            x2 = 2.0 * next_d(state) - 1.0
            r2 = x1 * x1 + x2 * x2
        f = np.sqrt(-2.0 * np.log(r2)  r2)
        out2 * i = f * x1
        if 2 * i + 1 < n
            out2 * i + 1 = f * x2
    return out

# Compile using Numba
normalsj = nb.jit(normals, nopython=True)
# Must use state address not state with numba
n = 10000

def numbacall():
    return normalsj(n, state_addr)

rg = np.random.Generator(PCG64())

def numpycall():
    return rg.normal(size=n)

# Check that the functions work
r1 = numbacall()
r2 = numpycall()
assert r1.shape == (n,)
assert r1.shape == r2.shape

t1 = timeit(numbacall, number=1000)
print('{:.2f} secs for {} PCG64 (Numba/PCG64) gaussian randoms'.format(t1, n))
t2 = timeit(numpycall, number=1000)
print('{:.2f} secs for {} PCG64 (NumPy/PCG64) gaussian randoms'.format(t2, n))

Оптимизация гиперпараметров. Раунд 1: RandomizedSearchCV

How to reverse a list in python

оптимизацией гиперпараметровздеськросс-валидаций

— число «деревьев» в «случайном лесу».
— число признаков для выбора расщепления.
— максимальная глубина деревьев.
— минимальное число объектов, необходимое для того, чтобы узел дерева мог бы расщепиться.
— минимальное число объектов в листьях.
— использование для построения деревьев подвыборки с возвращением.

Результаты работы алгоритма RandomizedSearchCV

Анализ значений гиперпараметров

: значения 300, 500, 700, видимо, показывают наилучшие средние результаты.
: маленькие значения, вроде 2 и 7, как кажется, показывают наилучшие результаты. Хорошо выглядит и значение 23. Можно исследовать несколько значений этого гиперпараметра, превышающих 2, а также — несколько значений около 23.
: возникает такое ощущение, что маленькие значения этого гиперпараметра дают более высокие результаты. А это значит, что мы можем испытать значения между 2 и 7.
: вариант даёт самый высокий средний результат.
: тут чёткой зависимости между значением гиперпараметра и результатом работы модели не видно, но есть ощущение, что значения 2, 3, 7, 11, 15 выглядят неплохо.
: значение показывает наилучший средний результат.

7.3. Статистика

Генераторы в python и их отличие от списков и функций

Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.

Элементарные статистические функции:

Средние значения элементов массива и их отклонения:

Корреляционные коэфициенты и ковариационные матрицы величин:

Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.

Генерация случайного n-мерного массива целых чисел

Для генерации случайного n-мерного массива целых чисел используется :

Python

import numpy

random_integer_array = numpy.random.random_integers(1, 10, 5)
print(«1-мерный массив случайных целых чисел \n», random_integer_array,»\n»)

random_integer_array = numpy.random.random_integers(1, 10, size=(3, 2))
print(«2-мерный массив случайных целых чисел \n», random_integer_array)

1
2
3
4
5
6
7
8

importnumpy

random_integer_array=numpy.random.random_integers(1,10,5)

print(«1-мерный массив случайных целых чисел \n»,random_integer_array,»\n»)

random_integer_array=numpy.random.random_integers(1,10,size=(3,2))

print(«2-мерный массив случайных целых чисел \n»,random_integer_array)

Вывод:

Shell

1-мерный массив случайных целых чисел

2-мерный массив случайных целых чисел

]

1
2
3
4
5
6
7

1-мерныймассивслучайныхцелыхчисел

101421

2-мерныймассивслучайныхцелыхчисел

910

Cython¶

Cython can be used to unpack the provided by a BitGenerator.
This example uses and the example from above. The usual caveats
for writing high-performance code using Cython – removing bounds checks and
wrap around, providing array alignment information – still apply.

#!/usr/bin/env python3
#cython: language_level=3
"""
This file shows how the to use a BitGenerator to create a distribution.
"""
import numpy as np
cimport numpy as np
cimport cython
from cpython.pycapsule cimport PyCapsule_IsValid, PyCapsule_GetPointer
from libc.stdint cimport uint16_t, uint64_t
from numpy.random cimport bitgen_t
from numpy.random import PCG64
from numpy.random.c_distributions cimport (
      random_standard_uniform_fill, random_standard_uniform_fill_f)


@cython.boundscheck(False)
@cython.wraparound(False)
def uniforms(Py_ssize_t n):
    """
    Create an array of `n` uniformly distributed doubles.
    A 'real' distribution would want to process the values into
    some non-uniform distribution
    """
    cdef Py_ssize_t i
    cdef bitgen_t *rng
    cdef const char *capsule_name = "BitGenerator"
    cdef double[::1 random_values

    x = PCG64()
    capsule = x.capsule
    # Optional check that the capsule if from a BitGenerator
    if not PyCapsule_IsValid(capsule, capsule_name):
        raise ValueError("Invalid pointer to anon_func_state")
    # Cast the pointer
    rng = <bitgen_t *> PyCapsule_GetPointer(capsule, capsule_name)
    random_values = np.empty(n, dtype='float64')
    with x.lock, nogil
        for i in range(n):
            # Call the function
            random_valuesi = rng.next_double(rng.state)
    randoms = np.asarray(random_values)

    return randoms

The BitGenerator can also be directly accessed using the members of the
struct.

@cython.boundscheck(False)
@cython.wraparound(False)
def uint10_uniforms(Py_ssize_t n):
    """Uniform 10 bit integers stored as 16-bit unsigned integers"""
    cdef Py_ssize_t i
    cdef bitgen_t *rng
    cdef const char *capsule_name = "BitGenerator"
    cdef uint16_t[::1 random_values
    cdef int bits_remaining
    cdef int width = 10
    cdef uint64_t buff, mask = x3FF

    x = PCG64()
    capsule = x.capsule
    if not PyCapsule_IsValid(capsule, capsule_name):
        raise ValueError("Invalid pointer to anon_func_state")
    rng = <bitgen_t *> PyCapsule_GetPointer(capsule, capsule_name)
    random_values = np.empty(n, dtype='uint16')
    # Best practice is to release GIL and acquire the lock
    bits_remaining = 
    with x.lock, nogil
        for i in range(n):
            if bits_remaining < width
                buff = rng.next_uint64(rng.state)
            random_valuesi = buff & mask
            buff >>= width

    randoms = np.asarray(random_values)
    return randoms

Cython can be used to directly access the functions in
. This requires linking with the
library located in .

def uniforms_ex(bit_generator, Py_ssize_t n, dtype=np.float64):
    """
    Create an array of `n` uniformly distributed doubles via a "fill" function.

    A 'real' distribution would want to process the values into
    some non-uniform distribution

    Parameters
    ----------
    bit_generator: BitGenerator instance
    n: int
        Output vector length
    dtype: {str, dtype}, optional
        Desired dtype, either 'd' (or 'float64') or 'f' (or 'float32'). The
        default dtype value is 'd'
    """
    cdef Py_ssize_t i
    cdef bitgen_t *rng
    cdef const char *capsule_name = "BitGenerator"
    cdef np.ndarray randoms

    capsule = bit_generator.capsule
    # Optional check that the capsule if from a BitGenerator
    if not PyCapsule_IsValid(capsule, capsule_name):
        raise ValueError("Invalid pointer to anon_func_state")
    # Cast the pointer
    rng = <bitgen_t *> PyCapsule_GetPointer(capsule, capsule_name)

    _dtype = np.dtype(dtype)
    randoms = np.empty(n, dtype=_dtype)
    if _dtype == np.float32
        with bit_generator.lock
            random_standard_uniform_fill_f(rng, n, <float*>np.PyArray_DATA(randoms))
    elif _dtype == np.float64
        with bit_generator.lock
            random_standard_uniform_fill(rng, n, <double*>np.PyArray_DATA(randoms))
    else
        raise TypeError('Unsupported dtype %r for random' % _dtype)
    return randoms

Introduction¶

The new infrastructure takes a different approach to producing random numbers
from the object. Random number generation is separated into
two components, a bit generator and a random generator.

The BitGenerator has a limited set of responsibilities. It manages state
and provides functions to produce random doubles and random unsigned 32- and
64-bit values.

The is the user-facing object that is nearly identical to
. The canonical method to initialize a generator passes a
bit generator as the sole argument.

from numpy.random import default_rng
rg = default_rng(12345)
rg.random()

One can also instantiate directly with a BitGenerator instance.
To use the older algorithm, one can instantiate it directly
and pass it to .

from numpy.random import Generator, MT19937
rg = Generator(MT19937(12345))
rg.random()

What’s New or Different

Warning

The Generator’s normal, exponential and gamma functions use 256-step Ziggurat
methods which are 2-10 times faster than NumPy’s Box-Muller or inverse CDF
implementations.
Optional argument that accepts or
to produce either single or double prevision uniform random variables for
select distributions
Optional argument that allows existing arrays to be filled for
select distributions
All BitGenerators can produce doubles, uint64s and uint32s via CTypes
is now the canonical way to generate integer
random numbers from a discrete uniform distribution. The and
methods are only available through the legacy .
The keyword can be used to specify open or closed intervals.
This replaces both and the deprecated .
is now the canonical way to generate floating-point
random numbers, which replaces ,
RandomState.sample, and RandomState.ranf. This is consistent with
Python’s .
All BitGenerators in numpy use to convert seeds into
initialized states.

See for a complete list of improvements and
differences from the traditional .

Shuffling a String

In this section, we will see how to shuffle string in Python. But it is not as simple as shuffling a list. If we try to rearrange a string’s characters using you will get an error.

The reason behind this is a string is immutable. And You can’t modify the immutable objects in Python. The function adjusts the position of the items. It changes the original object. The doesn’t’ work with String. I.e., It can’t accept string argument. Let’s understand this with the help of the following example.

You will get the

We have a solution to this. We can shuffle a string using various approaches. Let see each one by one.

Approach One

Convert String to list
Shuffle the list randomly
Convert the shuffled list into String

Output:

Original String:  pynative
shuffled String is:  anvtipye

Note: The above example shuffles the list in place. Let’s see how to get shuffled a list of the original list without changing it.

Approach Two: Shuffling a String, not in place

Using this approach, we can have the original string unchanged and get the new shuffled string in return. Also, we don’t need to convert string to list to get the shuffled string. i.e., To shuffle an immutable object like string and return a new shuffled string, we need to use instead.

Output:

Original String:  PYnative
shuffled String is:  vnYPatie