Радужная таблица

Введение

В то время как большинство проектов, связанных с компьютерной безопасностью, тратит много времени для взлома одного пароля шифровальных систем (простой перебор), RainbowCrack за время, сравнимое с временем взлома одного хэша простым перебором, получает таблицы хэшей, по которым с очень высокой вероятностью можно в тысячи раз быстрее взломать любой хэш из проверенного диапазона.

Обычно хэши и алгоритм хэширования известны всем, но обратное преобразование слишком сложно. На этом основывается безопасность многих систем.

Обладая отсортированной таблицей хэшей и соответствующей таблицей паролей, можно получить систему, позволяющую с помощью быстрого бинарного поиска по всем таблицам выполнить обратное преобразование хэша в пароль.

Стандартный клиент поддерживает следующие алгоритмы: LM, NTLM, MD5, SHA1, MYSQLSHA1, HALFLMCHALL, NTLMCHALL, ORACLE-SYSTEM и MD5-HALF, другие алгоритмы могут быть подключены в виде плагинов.

Etymology

The term, «Rainbow Tables,» was first used in Dr. Oechslin’s initial paper. The term refers to the way different reduction functions are used to increase the success rate of the attack. The original method by Hellman uses many small tables with a different reduction function each. Rainbow tables are much bigger and use a different reduction function in each column. When colors are used to represent the reduction functions, a rainbow appears in the rainbow table.

Figure 2 of Dr. Oechslin’s paper contains a black-and-white graphic that illustrates how these sections are related. For his presentation at the Crypto 2003 conference, Dr. Oechslin added color to the graphic in order to make the rainbow association more clear. The enhanced graphic that was presented at the conference is shown to the right.

Generate Rainbow Table with rtgen Program

Command line syntax of rtgen program:

rtgen hash_algorithm charset plaintext_len_min plaintext_len_max table_index chain_len chain_num part_index

An example to generate a rainbow table set with 6 rainbow tables:

rtgen md5 loweralpha-numeric 1 7 0 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 1 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 2 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 3 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 4 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 5 3800 33554432 0

Options:

hash_algorithm	Rainbow table is hash algorithm specific. Rainbow table for a certain hash algorithm only helps to crack hashes of that type. The rtgen program natively support lots of hash algorithms like lm, ntlm, md5, sha1, mysqlsha1, halflmchall, ntlmchall, oracle-SYSTEM and md5-half. In the example above, we generate md5 rainbow tables that speed up cracking of md5 hashes.
charset	The charset includes all possible characters for the plaintext. «loweralpha-numeric» stands for «abcdefghijklmnopqrstuvwxyz0123456789», which is defined in configuration file charset.txt.
plaintext_len_minplaintext_len_max	These two parameters limit the plaintext length range of the rainbow table. In the example above, the plaintext length range is 1 to 7. So plaintexts like «a» and «abcdefg» are likely contained in the rainbow table generated. But plaintext «abcdefgh» with length 8 will not be contained.
table_index1	The table_index parameter selects the reduction function. Rainbow table with different table_index parameter uses different reduction function.
chain_len1	This is the rainbow chain length. Longer rainbow chain stores more plaintexts and requires longer time to generate.
chain_num1	Number of rainbow chains to generate. Rainbow table is simply an array of rainbow chains. Size of each rainbow chain is 16 bytes.
part_index	To store a large rainbow table in many smaller files, use different number in this parameter for each part and keep all other parameters identical.

1 To fully understand the meaning of reduction function and the structure of rainbow table, reading of Philippe Oechslin’s paper is necessary.

There are many rainbow table characteristics determined implicitly by table generation parameters:

Table Size	With .rt rainbow table format, file size of a rainbow table equals to chain_num parameter multiplied by 16.
Key Space	Key space is the number of possible plaintexts, calculated based on number of characters in charset and plaintext length range parameters. In the example above, key space is 361 + 362 + 363 + 364 + 365 + 366 + 367 = 80603140212
Success Rate	The time-memory tradeoff algorithm is a probabilistic algorithm. Whatever the parameters are selected, there always exist many plaintexts (within the selected charset and plaintext length range) missing from the rainbow table generated. In the example above, success rate is 99.9% with all 6 rainbow tables. Success rate is determined by all table generation parameters except the hash_algorithm parameter.

To start generating the first rainbow table, run following command in a command window:

rtgen md5 loweralpha-numeric 1 7 0 3800 33554432 0

CPU will be busy computing rainbow chains. On system with multi-core processor, all cores are fully utilized.

To pause table generation, just press Ctrl+C and rtgen program will exit. Next time if the rtgen program is executed with exactly same parameters, table generation is resumed.

This command takes hours to complete with ordinary processor.

When finished, a file «md5_loweralpha-numeric#1-7_0_3800x33554432_0.rt» sized 512 MB is in current directory. The file name stores all table generation parameters.

Now generate the remaining 5 rainbow tables:

rtgen md5 loweralpha-numeric 1 7 1 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 2 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 3 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 4 3800 33554432 0
rtgen md5 loweralpha-numeric 1 7 5 3800 33554432 0

Finally, there are 6 rainbow tables generated:

536,870,912 md5_loweralpha-numeric#1-7_0_3800x33554432_0.rt
536,870,912 md5_loweralpha-numeric#1-7_1_3800x33554432_0.rt
536,870,912 md5_loweralpha-numeric#1-7_2_3800x33554432_0.rt
536,870,912 md5_loweralpha-numeric#1-7_3_3800x33554432_0.rt
536,870,912 md5_loweralpha-numeric#1-7_4_3800x33554432_0.rt
536,870,912 md5_loweralpha-numeric#1-7_5_3800x33554432_0.rt

Rainbow tables

We consider the problem of finding back a value from its hash (in the
current implementation, MD5). Formally, we want to perform a preimage
attack. Since hash functions are designed to be resistant to preimage
attacks, we are often reduced to brute forcing: consider every single
possible value, hash it and match it against the target hash. This is
guaranteed to work but can take tremendeous amounts of time.

For feasible targets, we can speed up the process by storing the result
of all these hashes in a (sorted) table. That way, whenever a new hash
comes in, we simply have to look it up in the table. However, lookup
tables tend to be huge and impractical.

Here, the hash 0e4f would be easily mapped to the value B.

The root idea of rainbow tables is to find a middle point between brute
force cracking and lookup tables. Instead of storing every value/hash
couples, they are grouped in «chains» each identified by one initial
value and one final hash. Basically, the hash of the initial value
is mapped to a new value, which is hashed in turn, mapped, and so on,
a fixed number of times, until a final hash.

In the example above, we choose to map hashes to values by taking the
first character of the hash and taking the corresponding letter of
the alphabet (e.g. ). Now, notice that we can freely choose the
initial values but the middle are already determined; some may not appear
(e.g. E) and some may appear twice (e.g. A). However, we do control the
mapping function so that we can optimize the repartition.

In this case, all that is actually stored is:

Now, if we are given some hash target (e.g. 12b2), we apply the map-hash
process until we find a matching value in the table and consider the chain
it belongs to. We then follow the chain until the value. In the example:

From the rainbow table, 3e4f corresponds to the chain beginning with B:

The mapping operation used in rainbow tables is called reduction.

Защита от радужных таблиц[править | править код]

Один из распространённых методов защиты от взлома с помощью радужных таблиц — использование необратимых хеш-функций, которые включают salt («соль», «модификатор»). Существует множество возможных схем смешения затравки и пароля. Например, рассмотрим следующую функцию для создания хеша от пароля:

хеш = MD5( пароль + соль ) 

Для восстановления такого пароля взломщику необходимы таблицы для всех возможных значений соли. При использовании такой схемы, соль должна быть достаточно длинной (6‒8 символов), иначе злоумышленник может вычислить таблицы для каждого значения соли, случайной и различной для каждого пароля. Таким образом два одинаковых пароля будут иметь разные значения хешей, если только не будет использоваться одинаковая соль.

По сути, соль увеличивает длину и, возможно, сложность пароля. Если таблица рассчитана на некоторую длину или на некоторый ограниченный набор символов, то соль может предотвратить восстановление пароля. Например, в старых Unix-паролях использовалась соль, размер которой составлял всего лишь 12 бит. Для взлома таких паролей злоумышленнику нужно было посчитать всего 4096 таблиц, которые можно свободно хранить на терабайтных жестких дисках. Поэтому в современных приложениях стараются использовать более длинную соль. Например, в алгоритме хеширования bcrypt используется соль размером 128 бит. Подобная длина соли делает предварительные вычисления просто бессмысленными. Другим возможным способом борьбы против атак, использующих предварительные вычисления, является растяжение ключа (англ. key stretching). Например:

ключ = хеш(пароль + соль) for 1 to 65536 do ключ = хеш(ключ + пароль + соль) 

Этот способ снижает эффективность применения предварительных вычислений, так как использование промежуточных значений увеличивает время, которое необходимо для вычисления одного пароля, и тем самым уменьшает количество вычислений, которые злоумышленник может произвести в установленные временные рамки. Данный метод применяется в следующих алгоритмах хеширования: MD5, в котором используется 1000 повторений, и bcrypt. Альтернативным вариантом является использование усиления ключа (англ. key strengthening), который часто принимают за растяжение ключа. Применяя данный метод, мы увеличиваем размер ключа за счёт добавки случайной соли, которая затем спокойно удаляется, в отличие от растяжения ключа, когда соль сохраняется и используется в следующих итерациях.

Introduction

This document explains the rcrack program. The rcrack program lookup existing rainbow tables for the plaintext of user supplied hash.

Six similar programs are available:

Program	User Interface	GPU Acceleration
rcrack	Command Line
rcrack_cuda	Command Line	NVIDIA CUDA
rcrack_cl	Command Line	AMD OpenCL
rcrack_gui	GUI
rcrack_cuda_gui	GUI	NVIDIA CUDA
rcrack_cl_gui	GUI	AMD OpenCL

Command line program is ideal for batch processing, and GUI program is easy to use.

Rainbow tables used by rcrack program must already be sorted with rtsort program, and optionally converted to .rtc file format with rt2rtc program.

Предрассчитанные цепочки хешей

Внимание: Цепочки хешей, описанные в этой статье, отличаются от описанных в статье Цепочка хешей.

Пусть у нас есть хеш-функция H с длиной хеша n и конечное множество паролей P. Наша цель — создать структуру данных, которая для любого значения хеша h может либо найти такой элемент p из P, что H(p)=h, либо определить, что такого элемента не существует. Простейший способ сделать это — вычислить H(p) для всех p из P, но для хранения такой таблицы потребуется Θ(|P|n) памяти, что слишком много.

Цепочки хешей — метод для уменьшения этого требования к объёму памяти. Главная идея — определение функции редукции R, которая сопоставляет значениям хеша значения из P. Заметим, что R не является обращением хеш-функции. Начиная с исходного пароля и попеременно применяя к каждому полученному значению H и R, мы получим цепочку перемежающихся паролей и хешей. Например, для набора паролей длиной в 6 символов и хеш-функции, выдающей 32-битные значения, цепочка может выглядеть так:

aaaaaa→H281DAF40→Rsgfnyd→H920ECF10→Rkiebgt{\displaystyle \mathbf {aaaaaa} \,{\xrightarrow{}}\,\mathrm {281DAF40} \,{\xrightarrow{}}\,\mathrm {sgfnyd} \,{\xrightarrow{}}\,\mathrm {920ECF10} \,{\xrightarrow{}}\,\mathbf {kiebgt} }

К функции редукции предъявляется единственное требование: возвращать значения из того же алфавита, что и пароли.

Для генерации таблицы мы выбираем случайное множество начальных паролей из P, вычисляем цепочки некоторой фиксированной длины k для каждого пароля и сохраняем только первый и последний пароль из каждой цепочки.

Для каждого хеша h, значение которого мы хотим обратить (найти соответствующий ему пароль), вычисляем последовательность R(…R(H(R(h)))…). Если какое-то из промежуточных значений совпадет с каким-нибудь концом какой-либо цепочки, мы берём начало этой цепочки и восстанавливаем её полностью. С высокой вероятностью полная цепочка будет содержать значение хеша h, а предшествующий ему пароль будет искомым.

Для примера, указанного выше, если у нас изначально есть хеш 920ECF10, он породит следующую последовательность:

920ECF10→Rkiebgt{\displaystyle \mathrm {920ECF10} \,{\xrightarrow{}}\,\mathbf {kiebgt} }

Поскольку является концом цепочки из нашей таблицы, мы берём соответствующий начальный пароль и вычисляем цепочку, пока не найдём хеш 920ECF10:

aaaaaa→H281DAF40→Rsgfnyd→H920ECF10{\displaystyle \mathbf {aaaaaa} \,{\xrightarrow{}}\,\mathrm {281DAF40} \,{\xrightarrow{}}\,\mathrm {sgfnyd} \,{\xrightarrow{}}\,\mathrm {920ECF10} }

Таким образом, искомый пароль — .

Стоит заметить, что восстановленная цепочка не всегда содержит искомое значение хеша h. Такое возможно при возникновении коллизии функции H или R. Например, пусть дан хеш FB107E70, который на определенном этапе порождает пароль kiebgt:

FB107E70→Rbvtdll→HEE80890→Rkiebgt{\displaystyle \mathrm {FB107E70} \,{\xrightarrow{}}\,\mathrm {bvtdll} \,{\xrightarrow{}}\,\mathrm {0EE80890} \,{\xrightarrow{}}\,\mathbf {kiebgt} }

Но FB107E70 не появляется в цепочке, порождённой паролем . Это называется ложным срабатыванием. В этом случае, мы игнорируем совпадение и продолжаем вычислять последовательность, порождённую h. Если сгенерированная последовательность достигает длины k без хороших совпадений, это означает, что искомый пароль никогда не встречался в предвычисленных цепочках.

Содержимое таблицы не зависит от значения обращаемого хеша, она вычисляется заранее и используется лишь для быстрого поиска. Увеличение длины цепочки уменьшает размер таблицы, но увеличивает время поиска нужного элемента в цепочке.

Простые цепочки хешей имеют несколько недостатков. Самый серьёзный — возможность слияния двух цепочек в одну (генерация одного и того же значения в разных цепочках). Все значения, сгенерированные после слияния, будут одинаковыми в обеих цепочках, что сужает количество покрываемых паролей. Поскольку прегенерированные цепочки сохраняются не целиком, невозможно эффективно сравнивать все сгенерированные значения между собой. Как правило, об отсутствии коллизий в хеш-функции H заботится сторона, обеспечивающая шифрование паролей, поэтому основная проблема кроется в функции редукции R.

Другая серьёзная проблема — подбор такой функции R, которая будет генерировать пароли с требуемым покрытием и распределением. Ограничение выходного алфавита является серьёзным ограничением для выбора такой функции.

How they work

Creating a table

Imagine we create a rainbow table with just two chains, each of length 5. The rainbow table is for the fictional hash function MD48, which outputs 48 bits (only 12 hexadecimal characters). When building the chain, we see this:

We start with because it’s the first chain (we just need some value to start with). When we hash this with MD48, it turns into . Now we apply a «reduce» function which basically formats this hash back into a password, and we end up with «z». When we hash that again, we get , then reduce it again and get . There are some more cycles, and the final result is .

Same for the second chain. We just start with another value and do the same thing. This ends in .

Our complete rainbow table is now this:

That’s all you have to store.

Looking up a hash

Let’s say we found a hash online, . Let’s crack it using our table!

To play around with it yourself, the above examples were created using this Python script: https://gist.github.com/lgommans/83cbb74a077742be3b31d33658f65adb

Время и память

Радужная таблица создаётся построением цепочек возможных паролей. Создание таких таблиц требует больше времени, чем нужно для создания обычных таблиц поиска, но значительно меньше памяти (вплоть до сотен гигабайт, при объёме для обычных таблиц в N слов для радужных нужно всего порядка N2/3). При этом они требуют хоть и больше времени (по сравнению с простыми методами вроде атаки по словарю) на восстановление исходного пароля, но на практике более реализуемы (для построения обычной таблицы для 6-символьного пароля с байтовыми символами потребуется 2566 = 281 474 976 710 656 блоков памяти, в то время как для радужной — всего 2566·⅔ = 4 294 967 296 блоков).

Таблицы могут взламывать только ту хеш-функцию, для которой они создавались, то есть таблицы для MD5 могут взломать только хеш MD5. Теория данной технологии была разработана Philippe Oechslin как быстрый вариант time-memory tradeoff. Впервые технология использована в программе Ophcrack для взлома хешей LanMan (LM-хеш), используемых в Microsoft Windows. Позже была разработана более совершенная программа RainbowCrack, которая может работать с большим количеством хешей, например, LanMan, MD5, SHA1 и другими.

Следующим шагом было создание программы The UDC, которая позволяет строить Hybrid Rainbow таблицы не по набору символов, а по набору словарей, что позволяет восстанавливать более длинные пароли (фактически неограниченной длины).

Background

Any computer system that requires password authentication must contain a database of passwords, either in plaintext or hashed in some form; therefore various techniques of exist. Because the tables are vulnerable to theft, storing the plaintext password is dangerous. Most databases, therefore, store a cryptographic hash of a user’s password in the database. In such a system, no one – including the authentication system – can determine what a user’s password is by merely looking at the value stored in the database. Instead, when a user enters a password for authentication, the system computes the hash value for the provided password, and that hash value is compared to the stored hash for that user. Authentication is successful if the two hashes match.

After gathering a password hash, using the said hash as a password would fail since the authentication system would hash it a second time. To learn a user’s password, a password that produces the same hashed value must be found, usually through a brute-force or dictionary attack.

Rainbow tables are one type of tool that have been developed to derive a password by looking only at a hashed value.

Rainbow tables are not always needed as there are more straightforward methods of plaintext recovery available. Brute-force attacks and dictionary attacks are the most straightforward methods available. However, these are not adequate for systems that use long passwords because of the difficulty of storing all the options available and searching through such an extensive database to perform a reverse lookup of a hash.

To address this issue of scale, reverse lookup tables were generated that stored only a smaller selection of hashes that when reversed could make long chains of passwords. Although the reverse lookup of a hash in a chained table takes more computational time, the lookup table itself can be much smaller, so hashes of longer passwords can be stored. Rainbow tables are a refinement of this chaining technique and provide a solution to a problem called chain collisions.

Defense against rainbow tables

A rainbow table is ineffective against one-way hashes that include large salts. For example, consider a password hash that is generated using the following function (where «+» is the concatenation operator):

Or

The salt value is not secret and may be generated at random and stored with the password hash. A large salt value prevents precomputation attacks, including rainbow tables, by ensuring that each user’s password is hashed uniquely. This means that two users with the same password will have different password hashes (assuming different salts are used). In order to succeed, an attacker needs to precompute tables for each possible salt value. The salt must be large enough, otherwise an attacker can make a table for each salt value. For older Unix passwords which used a 12-bit salt this would require 4096 tables, a significant increase in cost for the attacker, but not impractical with terabyte hard drives. The and methods—used in Linux, BSD Unixes, and Solaris—have salts of 128 bits. These larger salt values make precomputation attacks against these systems infeasible for almost any length of a password. Even if the attacker could generate a million tables per second, they would still need billions of years to generate tables for all possible salts.

Another technique that helps prevent precomputation attacks is key stretching. When stretching is used, the salt, password, and some intermediate hash values are run through the underlying hash function multiple times to increase the computation time required to hash each password. For instance, MD5-Crypt uses a 1000 iteration loop that repeatedly feeds the salt, password, and current intermediate hash value back into the underlying MD5 hash function. The user’s password hash is the concatenation of the salt value (which is not secret) and the final hash. The extra time is not noticeable to users because they have to wait only a fraction of a second each time they log in. On the other hand, stretching reduces the effectiveness of brute-force attacks in proportion to the number of iterations because it reduces the number of attempts an attacker can perform in a given time frame. This principle is applied in MD5-Crypt and in bcrypt. It also greatly increases the time needed to build a precomputed table, but in the absence of salt, this needs only be done once.

An alternative approach, called key strengthening, extends the key with a random salt, but then (unlike in key stretching) securely deletes the salt. This forces both the attacker and legitimate users to perform a brute-force search for the salt value. Although the paper that introduced key stretching referred to this earlier technique and intentionally chose a different name, the term «key strengthening» is now often (arguably incorrectly) used to refer to key stretching.

Rainbow tables and other precomputation attacks do not work against passwords that contain symbols outside the range presupposed, or that are longer than those precomputed by the attacker. However, tables can be generated that take into account common ways in which users attempt to choose more secure passwords, such as adding a number or special character. Because of the sizable investment in computing processing, rainbow tables beyond fourteen places in length are not yet common. So, choosing a password that is longer than fourteen characters may force an attacker to resort to brute-force methods.[citation needed]

Specific intensive efforts focused on LM hash, an older hash algorithm used by Microsoft, are publicly available. LM hash is particularly vulnerable because passwords longer than 7 characters are broken into two sections, each of which is hashed separately. Choosing a password that is fifteen characters or longer guarantees that an LM hash will not be generated.

Performance Tips

Memory Requirement

4 GB memory is minimal and 8 GB or more memory is recommended. Larger memory always help to improve performance when searching large rainbow tables.

Hard Disk

Because rainbow table must be loaded from hard disk to memory to look up and some rainbow table set can be as large as hundreds of GB, hard disk performance becomes a very important factor to achieve overall good hash cracking performance.

We suggest put rainbow tables in RAID 0 volume with multiple hard disks. Windows operating system natively support software RAID 0 called «striped volume».

The rcrack program always read data from hard disk sequentially. There is no random access.

Multiple GPUs

RainbowCrack software supports GPU acceleration with CUDA enabled GPUs from NVIDIA and OpenCL enabled GPUs from AMD.

GPU acceleration with multiple GPUs is supported. To get optimal performance, all GPUs need be of same model.

2020 RainbowCrack Project

Применение

При генерации таблиц важно найти наилучшее соотношения взаимосвязанных параметров:

• вероятность нахождения пароля по полученным таблицам;
• времени генерации таблиц;
• время подбора пароля по таблицам;
• занимаемое место.

Вышеназванные параметры зависят от настроек заданных при генерации таблиц:

• допустимый набор символов;
• длина пароля;
• длина цепочки;
• количество таблиц.

При этом время генерации зависит почти исключительно от желаемой вероятности подбора, используемого набора символов и длины пароля. Занимаемое таблицами место зависит от желаемой скорости подбора 1 пароля по готовым таблицам.

Хотя применение радужных таблиц облегчает использование полного перебора (то есть метода грубой силы — bruteforce) для подбора паролей, в некоторых случаях необходимые для их генерации/использования вычислительные мощности не позволяют одиночному пользователю достичь желаемых результатов за приемлемое время. К примеру, для паролей длиной не более 8 символов, состоящих из букв, цифр и специальных символов , захешированных алгоритмом MD5, могут быть сгенерированы таблицы со следующими параметрами:

• длина цепочки — 1400
• количество цепочек — 50 000 000
• количество таблиц — 800

При этом вероятность нахождения пароля с помощью данных таблиц составит 0,7542 (75,42 %), сами таблицы займут 596 ГиБ, генерация их на компьютере уровня Пентиум-3 1 ГГц займёт 3 года, а поиск 1 пароля по готовым таблицам — не более 22 минут.

Однако процесс генерации таблиц возможно распараллелить, например, расчёт одной таблицы с вышеприведёнными параметрами занимает примерно 33 часа. В таком случае, если в нашем распоряжении есть 100 компьютеров, все таблицы можно сгенерировать через 11 суток.

Радужные таблицы[править | править код]

Радужные таблицы являются развитием идеи таблицы хеш-цепочек. Они эффективно решают проблему коллизий путём введения последовательности функций редукции R₁, R₂, …, R_k. Функции редукции применяются по очереди, перемежаясь с функцией хеширования: H, R₁, H, R₂, …, H, R_k. При таком подходе две цепочки могут слиться только при совпадении значений на одной и той же итерации. Следовательно, достаточно проверять на коллизии только конечные значения цепочек, что не требует дополнительной памяти. На конечном этапе составления таблицы можно найти все слившиеся цепочки, оставить из них только одну и сгенерировать новые, чтобы заполнить таблицу необходимым количеством различных цепочек. Полученные цепочки не являются полностью свободными от коллизий, тем не менее, они не сольются полностью.

Использование последовательностей функций редукции изменяет способ поиска по таблице. Поскольку хеш может быть найден в любом месте цепочки, необходимо сгенерировать k различных цепочек:

• первая цепочка строится в предположении, что искомый хеш встретится на последней позиции в табличной цепочке, поэтому состоит из единственного значения R_k(h);
• вторая цепочка строится в предположении, что искомый хеш встретится на предпоследней позиции в табличной цепочке, поэтому выглядит так: R_k(H(R_k−1(h)));
• аналогично, наращивая длину цепочки и применяя функции редукции с меньшими номерами, получаем остальные цепочки. Последняя цепочка будет иметь длину k и содержать все функции редукции: R_k(H(R_k−1(H(…H(R₁(h))…))))

Также изменится и определение ложного срабатывания: если мы неверно «угадаем» позицию искомого хеша, это будет отбрасывать только одну из k сгенерированных цепочек; при этом всё ещё может оставаться возможность найти верный хеш для данной табличной цепочки, но на другой позиции.

Хотя радужные таблицы требуют отслеживания большего количества цепочек, они имеют бо́льшую плотность количества паролей на одну табличную запись. В отличие от таблицы хеш-цепочек, применение нескольких функций редукции уменьшает число потенциальных коллизий в таблице, что позволяет её наращивать без опасности получить большое количество слияний цепочек.

Примерправить | править код

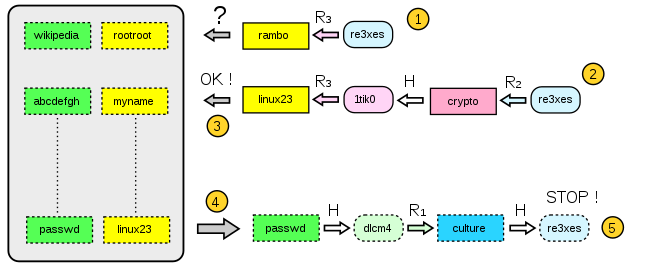
Имеется хеш (), который надо обратить (восстановить соответствующий пароль), и радужная таблица, полученная с использованием трёх функций редукции.

1. Вычисляем цепочку длины 1 от начального хеша: R₃(«re3xes»)=»rambo». Данный пароль не является концом ни одной табличной цепочки.
2. Вычисляем цепочку длины 2: R₃(H(R₂(«re3xes»)))=»linux23″.
3. Данный пароль найден в таблице. Берём начало найденной цепочки (пароль ).
4. Восстанавливаем табличную цепочку до тех пор, пока не получим исходный хеш .
5. Искомый хеш найден в цепочке, атака успешна. Предшествующий данному значению хеша пароль является искомым.

Теория Править

Радужная таблица создается построением цепочек возможных паролей. Каждая цепочка начинается со случайного возможного пароля, затем подвергается действию хеш-функции и функции редукции. Данная функция преобразует результат хеш-функции в некоторый возможный пароль. Промежуточные пароли в цепочке отбрасываются и в таблицу записывается только первый и последний элементы цепочек. Создание таблиц требует времени и памяти (вплоть до сотен гигабайт), но они позволяют очень быстро (по сравнению с обычными методами) восстановить исходный пароль.

Для восстановления пароля данное значение хеш-функции подвергается функции редукции и ищется в таблице. Если не было найдено совпадения, то снова применяется хеш-функция и функция редукции. Данная операция продолжается, пока не будет найдено совпадение. После нахождения совпадения, цепочка содержащая его, восстанавливается для нахождения отброшенного значения, которое и будет искомым паролем.

В итоге получается таблица, которая может с высокой вероятностью восстановить пароль за небольшое время.

Buy Rainbow Tables

Detailed information of the rainbow tables is available in this page.

NTLM Rainbow Tables (USD 900)

Includes:

• Rainbow Tables
  

  Table ID	Charset	Plaintext Length	Success Rate	Table Size
  lm_ascii-32-65-123-4#1-7	All 95 characters on standard keyboard	1 to 14	99.9 %	27 GB
  ntlm_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  ntlm_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  ntlm_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB

• RainbowCrack 1.8 software with AMD/NVIDIA GPU Acceleration
• One WD My Passport Ultra 2 TB (USB 3.0 and USB 2.0) hard drive containing the rainbow tables
• License in USB dongle
• Ship with

MD5 Rainbow Tables (USD 900)

Includes:

• Rainbow Tables
  

  Table ID	Charset	Plaintext Length	Success Rate	Table Size
  md5_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  md5_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  md5_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB

• RainbowCrack 1.8 software with AMD/NVIDIA GPU Acceleration
• One WD My Passport Ultra 2 TB (USB 3.0 and USB 2.0) hard drive containing the rainbow tables
• License in USB dongle
• Ship with

SHA1 Rainbow Tables (USD 900)

Includes:

• Rainbow Tables
  

  Table ID	Charset	Plaintext Length	Success Rate	Table Size
  sha1_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  sha1_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  sha1_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB

• RainbowCrack 1.8 software with AMD/NVIDIA GPU Acceleration
• One WD My Passport Ultra 2 TB (USB 3.0 and USB 2.0) hard drive containing the rainbow tables
• License in USB dongle
• Ship with

NTLM, MD5 and SHA1 Rainbow Tables (USD 2400)

Includes:

• Rainbow Tables
  

  Table ID	Charset	Plaintext Length	Success Rate	Table Size
  lm_ascii-32-65-123-4#1-7	All 95 characters on standard keyboard	1 to 14	99.9 %	27 GB
  ntlm_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  ntlm_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  ntlm_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB
  md5_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  md5_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  md5_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB
  sha1_ascii-32-95#1-8	All 95 characters on standard keyboard	1 to 8	96.8 %	460 GB
  sha1_mixalpha-numeric#1-9	a-z, A-Z, 0-9	1 to 9	96.8 %	690 GB
  sha1_loweralpha-numeric#1-10	a-z, 0-9	1 to 10	96.8 %	316 GB

• RainbowCrack 1.8 software with AMD/NVIDIA GPU Acceleration
• One Seagate BarraCuda 6TB ST6000DM003 (SATA) hard drive containing the rainbow tables
• License in USB dongle
• Ship with

2020 RainbowCrack Project

Выводы

На мой взгляд у сервиса PHE (как и у остальных сервисов) все же есть минус по сравнению с классическим подходом хеш+соль — добавляются точки отказа (сеть до сервиса, сервер с сервисом, сам сервис) и скорость выполнения операции увеличивается (как минимум за счет сетевого взаимодействия). Если использовать PHE сторонней компании как совершенно внешний сервис, то сюда добавляется еще сеть между датацентрами как точка отказа и дополнительное время на установление соединения и пересылку байтиков.

Тем не менее плюсы все же выглядят довольно вкусно:

• перебирать пароли как заверяют будет невозможно (или очень долго) без приватных ключей;
• в случае утечки базы или ключа достаточно обновить ключ и данные в базе (при должном умении это можно сделать бесшовно).

В общем, технология выглядит перспективно и я продолжу наблюдать за ней.

Спасибо Алексею Ермишкину Scratch и компании Virgil Security за то, что исследуете эту тему, делитесь информацией и публикуете исходные коды!

А как вы защищаете пароли (если не секрет)?