Анализ временных рядов. действительно ли российская экономика зависит от цен на газ?

Финальные заметки

В этой статье показано, как использовать Python для прогнозирования обменных курсов с использованием модели ARIMA. Финансовые рынки могут двигаться в любом направлении, и это делает очень трудным, если не невозможным, точное прогнозирование обменных курсов. При этом единственная цель прогнозирования обменных курсов через ARIMA — помочь нам в принятии взвешенных решений, которые максимизируют прибыль и минимизируют риски. Прогнозируемые обменные курсы зависят от допущений, налагаемых моделью ARIMA, которые основаны на понятиях авторегрессии, интегрированной и скользящей средней.

ARIMA — простая, но мощная модель. Предполагается, что исторические ценности диктуют поведение настоящего. Предполагается также, что данные не содержат аномалий, являются стационарными и параметры модели наряду с ошибкой являются постоянными.

Хотя ARIMA не воспринимает рыночные данные как исходные данные, экономические и политические условия или корреляцию всех факторов риска для прогнозирования обменных курсов, но простой пример, показанный выше, может быть полезен для прогнозирования движения стабильных валют в нормальных условиях, в которых поведение в прошлом диктует настоящее и ценности.

Пожалуйста, дайте мне знать, если у вас есть какие-либо отзывы.

Интересные факты

• Он является одним из тех двух людей (другим является Джузо Сузуя), что меньше чем за год добились звания следователя второго класса.
• У Аримы и Канеки Кена совпадает дата дня рождения.
• На обложке Тома 13, на очках Аримы, если присмотреться, то можно увидеть число “2”, отсылка к карте Таро — Верховная Жрица (II)
• В 21 главе манги «Tokyo Ghoul:re» Дайске Ато сравнивает Ариму с гениальным скрипачом еврейского происхождения Яшей Хейфецом, который своим талантом вызывал зависть и раздражение со стороны других скрипачей своей эры. То же наблюдалось и в случае с Аримой: его талант и гений стал причиной зависти и ревности, наполнивших других следователей по гулям.
• Однажды Кишо Арима убил гуля обычным зонтиком.
• В ходе одной из операций в 24-ом районе Кишо и вовсе заснул.

Операторное представление. Стационарность и единичные корни

Если ввести в рассмотрение лаговый оператор L Lxt=xt−1{\displaystyle L:~Lx_{t}=x_{t-1}}, тогда ARMA-модель можно записать следующим образом

Xt=c+(∑i=1pαiLi)Xt+(1+∑i=1qβiLi)εt{\displaystyle X_{t}=c+(\sum _{i=1}^{p}\alpha _{i}L^{i})X_{t}+(1+\sum _{i=1}^{q}\beta _{i}L^{i})\varepsilon _{t}}

или, перенеся авторегрессионную часть в левую часть равенства:

(1−∑i=1pαiLi)Xt=c+(1+∑i=1qβiLi)εt{\displaystyle (1-\sum _{i=1}^{p}\alpha _{i}L^{i})X_{t}=c+(1+\sum _{i=1}^{q}\beta _{i}L^{i})\varepsilon _{t}}

Введя сокращенные обозначения для полиномов левой и правой частей окончательно можно записать:

α(L)Xt=c+β(L)εt{\displaystyle \alpha (L)X_{t}=c+\beta (L)\varepsilon _{t}}

Для того, чтобы процесс был стационарным, необходимо, чтобы корни характеристического многочлена авторегрессионной части α(z){\displaystyle \alpha (z)} лежали вне единичного круга в комплексной плоскости (были по модулю строго больше единицы). Стационарный ARMA-процесс можно представить как бесконечный MA-процесс:

Xt=α−1(L)c+α−1(L)β(L)εt=ca(1)+∑i=∞ciεt−i{\displaystyle X_{t}=\alpha ^{-1}(L)c+\alpha ^{-1}(L)\beta (L)\varepsilon _{t}=c/a(1)+\sum _{i=0}^{\infty }c_{i}\varepsilon _{t-i}}

Например, процесс ARMA(1,0)=AR(1) можно представить как MA-процесс бесконечного порядка с коэффициентами убывающей геометрической прогрессии:

Xt=c(1−a)+∑i=∞aiεt−i{\displaystyle X_{t}=c/(1-a)+\sum _{i=0}^{\infty }a^{i}\varepsilon _{t-i}}

Таким образом, ARMA-процессы можно считать MA-процессами бесконечного порядка с определенными ограничениями на структуру коэффициентов. Малым количеством параметров они позволяют описать процессы достаточно сложной структуры. Все стационарные процессы можно сколь угодно приблизить ARMA-моделью некоторого порядка с помощью существенно меньшего числа параметров, нежели только при использовании MA-моделей.

Нестационарные (интегрированные) ARMA

Основная статья: ARIMA

При наличии единичных корней авторегрессионного полинома процесс является нестационарным. Корни меньше единицы на практике не рассматриваются, поскольку это процессы взрывного характера. Соответственно, для проверки стационарности временных рядов один из базовых тестов — тесты на единичные корни. Если тесты подтверждают наличие единичного корня, то анализируются разности исходного временного ряда и для стационарного процесса разностей некоторого порядка (обычно достаточно первого порядка, иногда второго) строится ARMA-модель. Такие модели называются ARIMA-моделями (интегрированный ARMA) или моделями Бокса-Дженкинса. Модель ARIMA(p, d, q), где d-порядок интегрирования (порядок разностей исходного временного ряда), p и q — порядок AR и MA — частей ARMA-процесса разностей d-го порядка, можно записать в следующей операторной форме

α(L)△dXt=c+β(L)εt ,   △=1−L{\displaystyle \alpha (L)\vartriangle ^{d}X_{t}=c+\beta (L)\varepsilon _{t}~,~~~\vartriangle =1-L}

Процесс ARIMA(p, d, q) эквивалентен процессу ARMA(p+d, q) с d единичными корнями.

Partial Auto Correlation Function (PACF)

As the name implies, PACF is a subset of ACF. PACF expresses the correlation between observations made at two points in time while accounting for any influence from other data points. We can use PACF to determine the optimal number of terms to use in the AR model. The number of terms determines the order of the model.

Let’s take a look at an example. Recall, that PACF can be used to figure out the best order of the AR model. The horizontal blue dashed lines represent the significance thresholds. The vertical lines represent the ACF and PACF values at in point in time. Only the vertical lines that exceed the horizontal lines are considered significant.

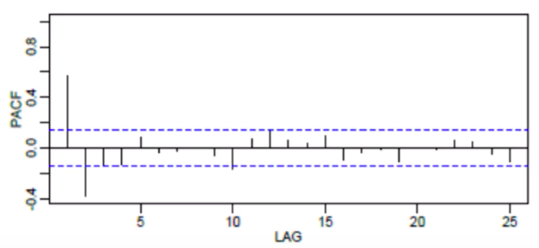
Thus, we’d use the preceding two days in the autoregression equation.

Recall, that ACF can be used to figure out the best order of the MA model.

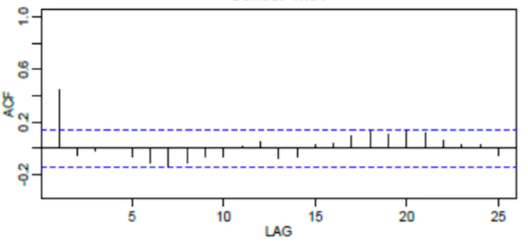
Thus, we’d only use yesterday in the moving average equation.

Going back to our example, we can create and fit an ARIMA model with AR of order 2, differencing of order 1 and MA of order 2.

decomposition = seasonal_decompose(df_log) model = ARIMA(df_log, order=(2,1,2))results = model.fit(disp=-1)plt.plot(df_log_shift)plt.plot(results.fittedvalues, color='red')

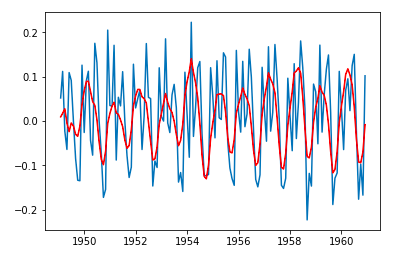
Then, we can see how the model compares to the original time series.

predictions_ARIMA_diff = pd.Series(results.fittedvalues, copy=True)predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()predictions_ARIMA_log = pd.Series(df_log.iloc, index=df_log.index)predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum, fill_value=0)predictions_ARIMA = np.exp(predictions_ARIMA_log)plt.plot(df)plt.plot(predictions_ARIMA)

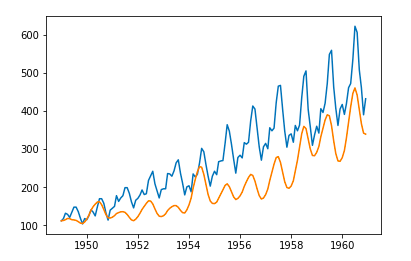
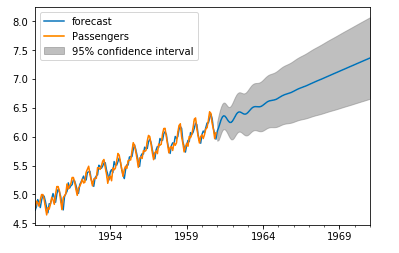
Given that we have data going for every month going back 12 years and want to forecast the number of passengers for the next 10 years, we use (12 x12)+ (12 x 10) = 264.

results.plot_predict(1,264)

Relevant information on Arrima

• Remember that the system based on the expression of interest has put an end to the intake order of “first come, first served” applications. It is possible to file an expression of interest form at any time, free of charge.
• It is advisable to use a personal computer or a tablet to access Arrima. The application does not allow navigation on a cell phone.
• You should use the latest version of one of the following browsers:
  • Google Chrome
  • Firefox
  • Safari
• You should also use one of the following operating systems:
  • Windows (version 8.1 and later)
  • Mac OS (version 10.2.4 and later)
  • iOS (version 11 and later)
• A virtual waiting room allows you to keep your place in the queue during peak periods. When you access the Arrima homepage, you may be automatically redirected to the virtual waiting room. You can then be informed about your position in the queue and the number of people waiting before you.
• Arrima is free. It is not necessary to hire the services of a remunerated person to fill out an expression of interest. If you choose to hire the services of a remunerated person, make sure that this person is a representative authorized by the Ministère.
• Any communication issued by the Ministère is carried out through the official channel: you will receive an e-mail notification when a communication is filed in the message center of your Arrima account. Be aware of unscrupulous individuals who may pose as government representatives; consult our notice on Internet fraud.

Модель авторегрессии с интегрированным скользящим средним

Модель ARIMAкласс статистических моделей для анализа и прогнозирования данных временных рядов.

Он явно обслуживает набор стандартных структур данных временных рядов и, как таковой, предоставляет простой, но мощный метод для создания искусных прогнозов временных рядов.

ARIMA — это аббревиатура от AutoRegressive Integrated Moving Average. Это обобщение более простой авторегрессионной скользящей средней и добавляет понятие интеграции.

Эта аббревиатура носит описательный характер и отражает ключевые аспекты самой модели. Вкратце, это:

• Арканзас:авторегрессии, Модель, которая использует зависимую связь между наблюдением и некоторым количеством запаздывающих наблюдений.
• я:интегрированный, Использование разности необработанных наблюдений (например, вычитание наблюдения из наблюдения на предыдущем временном шаге) для того, чтобы сделать временной ряд стационарным.
• Массачусетс:Скользящая средняя, Модель, которая использует зависимость между наблюдением и остаточной ошибкой от модели скользящего среднего, примененной к лаговым наблюдениям.

Каждый из этих компонентов явно указан в модели в качестве параметра. Используется стандартное обозначение ARIMA (p, d, q), где параметры заменяются целочисленными значениями для быстрого указания конкретной используемой модели ARIMA.

Параметры модели ARIMA определяются следующим образом:

• п: Число наблюдений отставания, включенных в модель, также называемое порядком отставания.
• d: Количество раз, когда исходные наблюдения различаются, также называется степенью различия.
• Q: Размер окна скользящей средней, также называемый порядком скользящей средней.

Построена модель линейной регрессии, включающая определенное количество и тип терминов, и данные подготавливаются по степени разности, чтобы сделать ее стационарной, то есть удалить трендовые и сезонные структуры, которые негативно влияют на модель регрессии.

Значение 0 может быть использовано для параметра, который указывает, что этот элемент модели не используется. Таким образом, модель ARIMA может быть сконфигурирована для выполнения функции модели ARMA и даже простой модели AR, I или MA.

Принятие модели ARIMA для временного ряда предполагает, что базовый процесс, который произвел наблюдения, является процессом ARIMA. Это может показаться очевидным, но помогает мотивировать необходимость подтверждения допущений модели в необработанных наблюдениях и в остаточных ошибках прогнозов из модели.

Далее, давайте посмотрим, как мы можем использовать модель ARIMA в Python. Начнем с загрузки простого одномерного временного ряда.

История

Ноутбук Arima, 1990

Arima Computer Corporation была основана в 1989 году. Компания специализировалась на выпуске компьютеров, в том числе ноутбуков. В 1994 году она выпустила акции, а в 1998 разместилась на Тайваньской фондовой бирже.

В 1999 году было основано подразделение Arima Communications, специализация которого — портативная электроника (мобильные телефоны, смартфоны).

В 2006 году Arima рассчитывала нарастить объёмы производства мобильных телефонов благодаря ODM-контрактам с японскими и европейскими производителями. Однако в 2007 году её показатели снизились, составив 9,5 млн устройств и 60,2 млн долларов прибыли. На 2008 год был запланирован рост: Arima выпускала устройства по заказу LG Electronics и Sony Ericsson (суммарно 90 % производства), а также для нескольких более мелких компаний. В 2008 году Arima избавилась от убыточного подразделения по ODM-производству ноутбуков и серверов, продав его Flextronics за 191,2 млн долларов.

В 2007 году были созданы подразделения Arima EcoEnergy Technologies и Arima Lasers, таким образом компания вышла на рынок оптоэлектроники и солнечной энергетики. В 2008 году она была переименована в Arima Photovoltaic & Optical Corporation.

В первом квартале 2011 года заказы Motorola составили 35-40 % от общего объёма отгрузок телефонов Arima, а доли Sony Ericsson и LG Electronics составили 30-35 % и 25-30 % соответственно.

Особенности модели

Сезонные и несезонные параметры должны удовлетворять неравенству:

C − (p + P + D + D·s) > 1

где:

• C.
  Длина исходного ряда;

• p.
  Максимальный порядок авторегрессии;

• P.
  Максимальный порядок сезонной авторегрессии;

• d.
  Разность;

• D.
  Сезонная разность;

• s.
  Период сезонности.

При наличии пропусков внутри исходного ряда количество используемых
для расчета значений уменьшается на n·(p + P
+ D + D·s), где n
— количество пропусков в исходном ряде.

Модель ARIMA предполагает, что
ϵt
— последовательность независимых одинаково распределенных случайных величин,
имеющих нормальное распределение вероятностей с нулевым математическим
ожиданием и некоторой дисперсией σ2.
Если после оценивания параметров это предположение не выполняется, то
выбранная спецификация модели некорректна.

Необходимо отметить, что модель ARMA
предполагает стационарность моделируемого ряда. В таком случае все корни
характеристических уравнений для процессов авторегрессии и скользящего
среднего должны лежать внутри единичного круга в комплексной плоскости.

Корни для AR-процесса находятся из уравнения:

Корни для MA-процесса находятся из уравнения

Если после оценивания параметров предположение о том, что корни лежат
внутри единичного круга, не выполняется, то полученный процесс является
нестационарным.

См. также:

Библиотека
методов и моделей | Модель регрессии
с авторегрессионными остатками и скользящим средним | Оценка
коэффициентов модели ARIMA | Контейнер моделирования: модель «ARIMA»
| Анализ временных рядов: ARIMA
| IModelling.Arima |
IEmARIMASettings
| ISmLinearRegress

Справочная
система на версию 9.2
Update 14 от 25/08/2020,
ООО «ФОРСАЙТ»,

Теория временных рядов

Мы тут не за теорией, но некоторые основные понятия ввести тем не менее надо. За более глубоким разъяснением советую обратиться к учебникам Светуньковых (у них, кстати, есть сайт c блогом).

Итак, под временным рядом понимаются последовательно измеренные через некоторые (зачастую равные) промежутки времени данные. Например, люди на протяжении ста лет измерядли тепрературу воздуха в каком-то мести и получили временной ряд. Самое ценное, что можно делать с временными рядами — это прогнозировать их дальнейшние значения. Прогноз — это всегда вероятностное, но научно обоснованное суждение о созможных будущих состояниях объекта или явления, в нём всегда есть доля ошибки. В лучшем случае эта ошибка случайная, в худшем — систематическая (о видах ошибок читайте в лекции «честные модели»). Чтобы построить прогноз необходима математическая модель, которая задаст правило для его расчёта, причём эта модель будет стохастической, поскольку в ней обязательно присутствует неопределённость в виде ошибки.

Помимо этого на временных рядах можно тестировать различные гипотезы: есть ли между двумя временными рядами связь, являются ли они стационарными или нет. Стационарность — это свойство процесса не менять свои характеристики со временем, т.е. если во временном ряду есть какой-либо тренд, он уже не стационарен. Это неудобно, поскольку многие модели и тесты предполагают стационарность временных рядов, а на нестационарных рядах их результаты ненадёжны.

6: Прогнозирование временных рядов

Теперь у вас есть модель временных рядов, с помощью которой можно спрогнозировать данные.

Для начала нужно сравнить прогнозируемые значения с реальными значениями временного ряда, что поможет нам понять точность прогнозов. Атрибуты get_prediction () и conf_int () позволяют получать значения и интервалы для прогнозов временных рядов.

Данный код начнёт прогнозирование с января 1998.

Аргумент dynamic=False включает пошаговое прогнозирование, а это означает, что прогнозы в каждой точке генерируются с использованием полной истории вплоть до этой точки.

Визуализируйте реальные и прогнозируемые значения временного ряда CO2, чтобы оценить, как всё работает

Обратите внимание, в конце временного ряда нужно изменить масштаб, для этого создаётся срез индекса даты

В целом, прогнозы соответствуют истинным значениям, демонстрируя общий тренд на увеличение.

Также полезно оценить точность наших прогнозов. Для этого можно использовать MSE (Mean Squared Error), что суммирует среднюю ошибку прогнозов. Для каждого прогнозируемого значения нужно вычислить его расстояние до истинного значения. Результаты нужно возводить в квадрат, чтобы различия не компенсировали друг друга при вычислении общего среднего.

MSE прогнозов на один шаг вперед дает значение 0,07 (это очень низкое значение, так как оно близко к 0). MSE 0 означает, что прогноз составлен с идеальной точностью. К этому результату и нужно стремиться, но его не всегда возможно достичь.

Более точное представление точности прогнозирования может быть получено с помощью динамических прогнозов. В этом случае нужно использовать только информацию из временных рядов до определенной точки; затем прогнозы сгенерируются с помощью значений из предыдущих прогнозируемых временных точек.

Данный код начнёт динамическое прогнозирование с января 1998 года.

Отобразив существующие и прогнозируемые значения временного ряда, обратите внимание: общие прогнозы точны даже при динамическом построении. Все прогнозируемые значения (красная линия) очень близко находятся к реальным (синяя линия), а значит, соответствуют истине

Кроме того, они находятся в пределах интервалов.

Чтобы узнать точность прогноза, вычислите MSE:

Прогнозируемые данные вернули MSE 1.01. Это немного больше, чем в предыдущем разделе (чего следовало ожидать, учитывая, что здесь используются менее точные данные временных рядов).

Как пошаговый прогноз, так и динамические прогнозы подтверждают, что эта модель временного ряда работает. Теперь можно попробовать спрогнозировать будущие значения ряда.

Просмотреть среднеквадратичную ошибку

Я также импортировал дополнительную библиотеку sklearn который я буду использовать в своих будущих блогах.

Скопируйте и вставьте эту строку:

«Из sklearn.metrics import mean_squared_error» для импорта библиотеки.

Наконец, напечатайте Mean Squared Error:

Среднеквадратичная ошибка вычисляет среднее значение разницы между фактическими и прогнозируемыми данными и говорит вам, насколько хороша ваша модель. Больше информации можно найти в моем блоге: Насколько хороша моя прогнозирующая модель — регрессионный анализ

Запустив приведенный ниже код, мы можем просмотреть фактические, прогнозируемые значения вместе с линейным графиком и общей среднеквадратичной ошибкой:

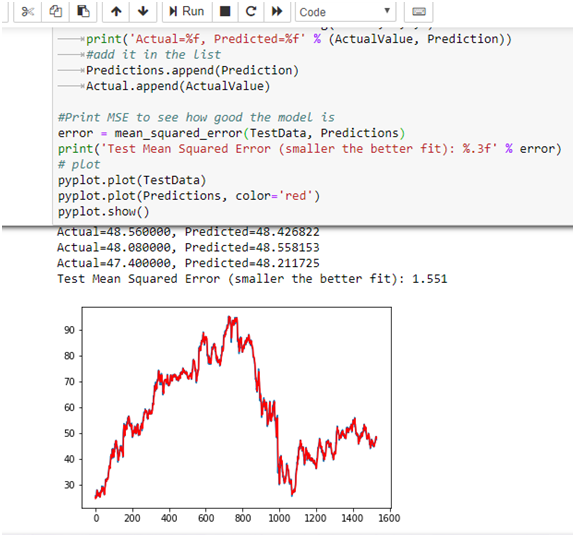
Как видите, мы напечатали фактические и прогнозные значения. Кроме того, мы построили прогнозируемые значения в красном с MSE 1,555.

Для полной тетради, пожалуйста, посетите здесь.

How does it work?

Anyone wishing to immigrate to Quйbec under the Regular Skilled Worker Program must go through Arrima.

The Arrima immigration application management system is based on an expression of interest and follows a three-step process:

1. First, you must complete an expression of interest form online. You will need to enter certain information, such as your education, language skills, and work experience.
2. The Ministère reviews the bank of expressions of interest and issues invitations to applicants who meet certain criteria, based on labour market needs in the different regions of Québec. Those individuals can submit a permanent selection application (official immigration application) and pay the associated fees.
3. Applications will be evaluated using the selection grid in effect.

Example¶

We’ll run an ARIMA Model for yearly sunspot data. First we load the data:

import numpy as np
import pandas as pd
import pyflux as pf
from datetime import datetime
import matplotlib.pyplot as plt
%matplotlib inline

data = pd.read_csv('https://vincentarelbundock.github.io/Rdatasets/csv/datasets/sunspot.year.csv')
data.index = data'time'.values

plt.figure(figsize=(15,5))
plt.plot(data.index,data'sunspot.year'])
plt.ylabel('Sunspots')
plt.title('Yearly Sunspot Data');

We can build an ARIMA model as follows, specifying the order of model we want, as well as a pandas DataFrame or numpy array carrying the data. Here we specify an arbitrary \(ARIMA(4,0,4)\) model:

model = pf.ARIMA(data=data, ar=4, ma=4, target='sunspot.year', family=pf.Normal())

Next we estimate the latent variables. For this example we will use a maximum likelihood point mass estimate \(z^{MLE}\):

x = model.fit("MLE")
x.summary()

ARIMA(4,,4)
======================================== ============================================
Dependent Variable sunspot.year         Method MLE
Start Date 1704                         Log Likelihood -1189.488
End Date 1988                           AIC 2398.9759
Number of observations 285              BIC 2435.5008
=====================================================================================
Latent Variable      Estimate   Std Error  z        P>|z|    95% C.I.
==================== ========== ========== ======== ======== ========================
Constant             8.0092     3.2275     2.4816   0.0131   (1.6834 | 14.3351)
AR(1)                1.6255     0.0367     44.2529  0.0      (1.5535 | 1.6975)
AR(2)                -0.4345    0.2455     -1.7701  0.0767   (-0.9157 | 0.0466)
AR(3)                -0.8819    0.2295     -3.8432  0.0001   (-1.3317 | -0.4322)
AR(4)                0.5261     0.0429     12.2515  0.0      (0.4419 | 0.6103)
MA(1)                -0.5061    0.0383     -13.2153 0.0      (-0.5812 | -0.4311)
MA(2)                -0.481     0.1361     -3.533   0.0004   (-0.7478 | -0.2142)
MA(3)                0.2511     0.1093     2.2979   0.0216   (0.0369 | 0.4653)
MA(4)                0.2846     0.0602     4.7242   0.0      (0.1665 | 0.4027)
Sigma                15.7944
=====================================================================================

We can plot the latent variables \(z^{MLE}\): using the : method:

model.plot_z(figsize=(15,5))

We can plot the in-sample fit using :

model.plot_fit(figsize=(15,10))

We can get an idea of the performance of our model by using rolling in-sample prediction through the : method:

model.plot_predict_is(h=50, figsize=(15,5))

If we want to plot predictions, we can use the : method:

model.plot_predict(h=20,past_values=20,figsize=(15,5))

Мастер настройки

Шаг 1. Настройка входных столбцов

На первом этапе необходимо задать назначение столбцов входного набора данных. Для каждого из столбцов можно выбрать один из вариантов назначения:

• Прогнозируемое — для данных, соответствующих временному ряду.
• Входное — для данных, соответствующих дополнительным входным факторам.
• Не задано — для данных, не участвующих в построении модели. Устанавливается по умолчанию для остальных столбцов.

Шаг 2. Настройки нормализации

Для моделей ARIMA нормализация для прогнозируемых данных обычно не требуется. Рекомендуется не применять нормализацию для данных временного ряда, для данных внешних факторов не менять настройки по умолчанию.

Структура модели ARIMAX

• Определить структуру автоматически — при установке данного флага активируется автоподбор параметров модели. Параметры в процессе вычисления подбираются таким образом, чтобы минимизировать значение AIC.
• Порядок AR части — задает порядок (р) авторегрессионной части. Определяет число предыдущих значений ряда, учитываемых при построении модели. Устанавливается значение целого типа больше 0.
• Порядок интегрирования — задает порядок (d) разностей ряда при необходимости привести исходный ряд к стационарному. Устанавливается значение целого типа больше 0.
• Порядок MA части — задает порядок (q) части скользящего среднего. Определяет размер скользящего окна для сглаживания исходного ряда. Устанавливается значение целого типа больше 0.
• Включить расчет сезонности — установка данного флага позволяет задать параметры для сезонной составляющей:
  • Порядок сезонной AR части — устанавливает значение целого типа от 0 и выше.
  • Порядок сезонного интегрирования — устанавливает значение целого типа от 0 и выше.
  • Порядок сезонной MA части — устанавливает значение целого типа от 0 и выше.
  • Период сезонной составляющей — устанавливает положительное значение целого типа.
• Включить константу в модель — значение логического типа. По умолчанию включено.

Прогнозирование временных рядов

• Горизонт прогноза — задает количество значений, которые будут спрогнозированы и добавлены в выходной набор в конце исходного временного ряда. Устанавливает значение целого типа больше 1.
• Рассчитать ошибку аппроксимации — флаг, установка которого добавляет в выходной набор столбец со средними отклонениями прогнозируемых значений от фактических.
• Рассчитать доверительный интервал

  Доверительный интервал прогноза в % от 0 до 100 — значение вещественного типа, по умолчанию 95.

  — позволяет вручную задать настройку следующего параметра: