Списки (list). функции и методы списков
Содержание:
Взаимообмен узлов ДЛС
В качестве аргументов функция взаимообмена узлов ДЛС принимает два указателя на обмениваемые узлы, а также указатель на корень списка. Функция возвращает адрес корневого узла списка.
Взаимообмен узлов списка осуществляется путем переустановки указателей. Для этого необходимо определить предшествующий и последующий узлы для каждого заменяемого. При этом возможны две ситуации:
- заменяемые узлы являются соседями;
- заменяемые узлы не являются соседями, то есть между ними имеется хотя бы один узел.
При замене соседних узлов переустановка указателей выглядит следующим образом:
При замене узлов, не являющихся соседними переустановка указателей выглядит следующим образом:
Функция взаимообмена узлов списка выглядит следующим образом:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051
struct list * swap(struct list *lst1, struct list *lst2, struct list *head){ // Возвращает новый корень списка struct list *prev1, *prev2, *next1, *next2; prev1 = lst1->prev; // узел предшествующий lst1 prev2 = lst2->prev; // узел предшествующий lst2 next1 = lst1->next; // узел следующий за lst1 next2 = lst2->next; // узел следующий за lst2 if (lst2 == next1) // обмениваются соседние узлы { lst2->next = lst1; lst2->prev = prev1; lst1->next = next2; lst1->prev = lst2; if(next2 != NULL) next2->prev = lst1; if (lst1 != head) prev1->next = lst2; } else if (lst1 == next2) // обмениваются соседние узлы { lst1->next = lst2; lst1->prev = prev2; lst2->next = next1; lst2->prev = lst1; if(next1 != NULL) next1->prev = lst2; if (lst2 != head) prev2->next = lst1; } else // обмениваются отстоящие узлы { if (lst1 != head) // указатель prev можно установить только для элемента, prev1->next = lst2; // не являющегося корневым lst2->next = next1; if (lst2 != head) prev2->next = lst1; lst1->next = next2; lst2->prev = prev1; if (next2 != NULL) // указатель next можно установить только для элемента, next2->prev = lst1; // не являющегося последним lst1->prev = prev2; if (next1 != NULL) next1->prev = lst2; } if (lst1 == head) return(lst2); if (lst2 == head) return(lst1); return(head);}
Код примера использования приведенных функцийСтруктуры данных
Методы списков
Давайте теперь
предположим, что у нас имеется список из чисел:
a = 1, -54, 3, 23, 43, -45,
и мы хотим в
конец этого списка добавить значение. Это можно сделать с помощью метода:
a.append(100)
И обратите
внимание: метод append ничего не возвращает, то есть, он меняет
сам список благодаря тому, что он относится к изменяемому типу данных. Поэтому
писать здесь конструкцию типа
a = a.append(100)
категорически не
следует, так мы только потеряем весь наш список! И этим методы списков
отличаются от методов строк, когда мы записывали:
string="Hello" string = string.upper()
Здесь метод upper возвращает
измененную строку, поэтому все работает как и ожидается. А метод append ничего не
возвращает, и присваивать значение None переменной a не имеет
смысла, тем более, что все работает и так:
a = 1, -54, 3, 23, 43, -45, a.append(100)
Причем, мы в методе
append можем записать
не только число, но и другой тип данных, например, строку:
a.append("hello")
тогда в конец
списка будет добавлен этот элемент. Или, булевое значение:
a.append(True)
Или еще один
список:
a.append(1,2,3)
И так далее. Главное,
чтобы было указано одно конкретное значение. Вот так работать не будет:
a.append(1,2)
Если нам нужно
вставить элемент в произвольную позицию, то используется метод
a.insert(3, -1000)
Здесь мы
указываем индекс вставляемого элемента и далее значение самого элемента.
Следующий метод remove удаляет элемент
по значению:
a.remove(True)
a.remove('hello')
Он находит
первый подходящий элемент и удаляет его, остальные не трогает. Если же
указывается несуществующий элемент:
a.remove('hello2')
то возникает
ошибка. Еще один метод для удаления
a.pop()
выполняет
удаление последнего элемента и при этом, возвращает его значение. В самом
списке последний элемент пропадает. То есть, с помощью этого метода можно
сохранять удаленный элемент в какой-либо переменной:
end = a.pop()
Также в этом
методе можно указывать индекс удаляемого элемента, например:
a.pop(3)
Если нам нужно
очистить весь список – удалить все элементы, то можно воспользоваться методом:
a.clear()
Получим пустой
список. Следующий метод
a = 1, -54, 3, 23, 43, -45, c = a.copy()
возвращает копию
списка. Это эквивалентно конструкции:
c = list(a)
В этом можно
убедиться так:
c1 = 1
и список c будет отличаться
от списка a.
Следующий метод count позволяет найти
число элементов с указанным значением:
c.count(1) c.count(-45)
Если же нам
нужен индекс определенного значения, то для этого используется метод index:
c.index(-45) c.index(1)
возвратит 0,
т.к. берется индекс только первого найденного элемента. Но, мы здесь можем
указать стартовое значение для поиска:
c.index(1, 1)
Здесь поиск
будет начинаться с индекса 1, то есть, со второго элемента. Или, так:
c.index(23, 1, 5)
Ищем число 23 с
1-го индекса и по 5-й не включая его. Если элемент не находится
c.index(23, 1, 3)
то метод
приводит к ошибке. Чтобы этого избежать в своих программах, можно вначале
проверить: существует ли такой элемент в нашем срезе:
23 in c1:3
и при значении True далее уже
определять индекс этого элемента.
Следующий метод
c.reverse()
меняет порядок
следования элементов на обратный.
Последний метод,
который мы рассмотрим, это
c.sort()
выполняет
сортировку элементов списка по возрастанию. Для сортировки по убыванию, следует
этот метод записать так:
c.sort(reverse=True)
Причем, этот
метод работает и со строками:
lst = "Москва", "Санкт-Петербург", "Тверь", "Казань" lst.sort()
Здесь
используется лексикографическое сравнение, о котором мы говорили, когда
рассматривали строки.
Это все основные
методы списков и чтобы вам было проще ориентироваться, приведу следующую
таблицу:
|
Метод |
Описание |
|
append() |
Добавляет |
|
insert() |
Вставляет |
|
remove() |
Удаляет |
|
pop() |
Удаляет |
|
clear() |
Очищает |
|
copy() |
Возвращает |
|
count() |
Возвращает |
|
index() |
Возвращает |
|
reverse() |
Меняет |
|
sort() |
Сортирует |
How to find an element in a C# List?
The IndexOf method finds an item in a List. The IndexOf method returns -1 if there are no items found in the List.
The following code snippet finds a string and returns the matched position of the item.
- int idx = authors.IndexOf(«Naveen Sharma»);
- if (idx > 0)
- Console.WriteLine($»Item index in List is: {idx}»);
- else
- Console.WriteLine(«Item not found»);
We can also specify the position in a List where IndexOf method can start searching from.
For example, the following code snippet finds a string starting at the 3rd position in a String.
- Console.WriteLine(authors.IndexOf(«Naveen Sharma», 2));
The LastIndexOf method finds an item from the end of List.
The following code snippet looks for a string in the backward direction and returns the index of the item if found.
- Console.WriteLine(authors.LastIndexOf(«Mahesh Chand»));
The complete example is listed in Listing 7.
- List<string> authors = new List<string>(5);
- authors.Add(«Mahesh Chand»);
- authors.Add(«Chris Love»);
- authors.Add(«Allen O’neill»);
- authors.Add(«Naveen Sharma»);
- authors.Add(«Mahesh Chand»);
- authors.Add(«Monica Rathbun»);
- authors.Add(«David McCarter»);
- int idx = authors.IndexOf(«Naveen Sharma»);
- if (idx > 0)
- Console.WriteLine($»Item index in List is: {idx}»);
- else
- Console.WriteLine(«Item not found»);
- Console.WriteLine(authors.IndexOf(«Naveen Sharma», 2));
- Console.WriteLine(authors.LastIndexOf(«Mahesh Chand»));
Listing 7.
How to remove items from a C# List?
The List class provides Remove methods that can be used to remove an item or a range of items.
The Remove method removes the first occurrence of the given item in the List. The following code snippet removes the first occurrence of ‘New Author1’.
- authors.Remove(«New Author1»);
The RemoveAt method removes an item at the given position. The following code snippet removes the item at the 3rd position.
- authors.RemoveAt(3);
The RemoveRange method removes a list of items from the starting index to the number of items. The following code snippet removes two items starting at 3rd position.
- authors.RemoveRange(3, 2);
The Clear method removes all items from a List<T>. The following code snippet removes all items from a List.
- authors.Clear();
Сортировка List в языке C#
Для того, чтобы произвести сортировку списка List, элементами которого являются ссылочные типы данных, сначала необходимо написать метод, описывающий сравнение двух таких “сложных” элементов списка.
Данный метод называется Compare и он должен находиться в отдельно созданном классе, реализующем интерфейс IComparer<>.
Первый пример сортировки списка
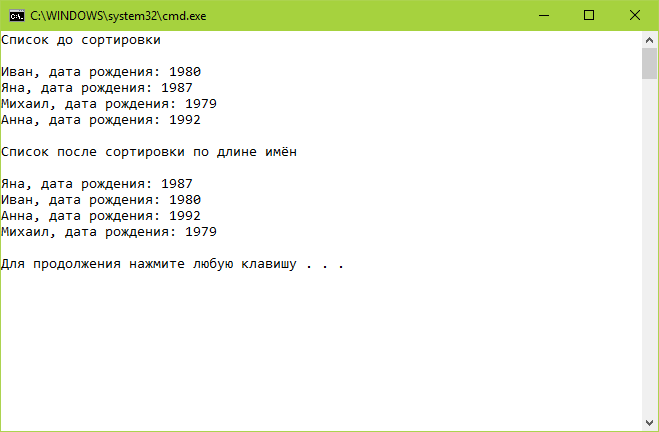
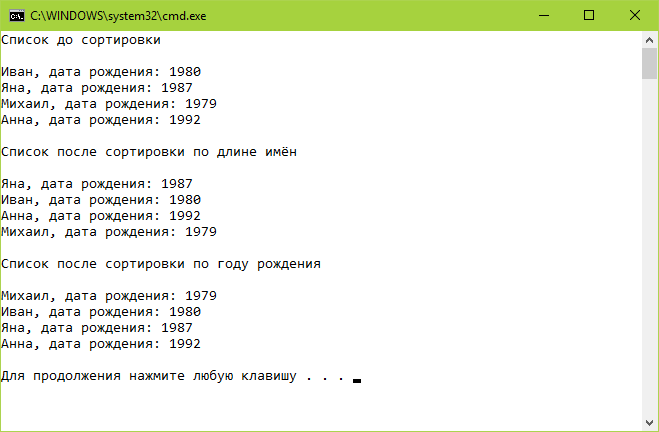
Сначала выполним сортировку по такому принципу: отсортируем список people по возрастанию длин имён людей.
Для этого создадим класс с именем NameComparer (имя может быть любым допустимым), который реализует интерфейс IComparer<string[]>. Тип string[] мы указываем, поскольку элемент списка в нашем случаем – это строковый массив.
C#
class NameComparer : IComparer<string[]>
{
public int Compare(string[] o1, string[] o2)
{
if (o1.Length > o2.Length)
{
return 1;
}
else if (o1.Length < o2.Length)
{
return -1;
}
return 0;
}
}
|
1 |
classNameComparerIComparer<string> { publicintCompare(stringo1,stringo2) { if(o1.Length>o2.Length) { return1; } elseif(o1.Length<o2.Length) { return-1; } return; } } |
В классе обязательно должен содержаться метод Compare, в котором описано как сравнивать два объекта (два элемента списка). В нашем случае эти объекты имеют имена o1 и o2.
Сортировка по возрастанию
Если первый объект по нужному признаку больше второго объекта, то следует возвратить единицу. Если меньше, то минус единицу.
Если объекты равны, то возвращаем ноль.
Для сортировки по убыванию поменяйте местами 1 и -1.
В данном примере мы сравниваем длину строк первых (нулевых) элементов двух массивов, поскольку в первом элементе хранится имя пользователя.
Отсортируем список people. Для этого создадим экземпляр класса NameComparer и вызовем у списка метод Sort, передав в него в качестве аргумента экземпляр созданного класса. После выведем список в консоль.
C#
NameComparer nc = new NameComparer();
people.Sort(nc);
OutputList(people, «Список после сортировки по длине имён»);
|
1 |
NameComparer nc=newNameComparer(); people.Sort(nc); OutputList(people,»Список после сортировки по длине имён»); |
 Второй пример сортировки списка
Второй пример сортировки списка
Рассмотрим еще один пример сортировки. На этот раз отсортируем список people по году рождения людей (от старших к младшим). Для этого создадим класс YearComparer.
C#
class YearComparer : IComparer<string[]>
{
public int Compare(string[] o1, string[] o2)
{
int a = Convert.ToInt32(o1);
int b = Convert.ToInt32(o2);
if (a > b)
{
return 1;
}
else if (a < b)
{
return -1;
}
return 0;
}
}
|
1 |
classYearComparerIComparer<string> { publicintCompare(stringo1,stringo2) { inta=Convert.ToInt32(o11); intb=Convert.ToInt32(o21); if(a>b) { return1; } elseif(a<b) { return-1; } return; } } |
Поскольку у нас год хранится в виде строки, сначала её необходимо конвертировать в число. Делается это с помощью метода Convert.ToInt32() .
Отсортируем List по годам рождения пользователей и выведем его на экран.
C#
YearComparer yc = new YearComparer();
people.Sort(yc);
OutputList(people, «Список после сортировки по году рождения»);
|
1 |
YearComparer yc=newYearComparer(); people.Sort(yc); OutputList(people,»Список после сортировки по году рождения»); |
Скачать исходник программы из данного урока:
Скачать исходникРепозиторий проекта на GitHub
How to create List in C#?
List is a generic class and is defined in the System.Collections.Generic namespace. You must import this namespace in your project to access the List<T> class.
- using System.Collections.Generic;
List<T> class constructor is used to create a List object of type T. It can either be empty or take an Integer value as an argument that defines the initial size of the list, also known as capacity. If there is no integer passed in the constructor, the size of the list is dynamic and grows every time an item is added to the array. You can also pass an initial collection of elements when initialize an object.
The code snippet in Listing 1 creates a List of Int16 and a list of string types. The last part of the code creates a List<T> object with an existing collection.
- List<Int16> list = new List<Int16>();
- List<string> authors = new List<string>(5);
- string[] animals = { «Cow», «Camel», «Elephant» };
- List<string> animalsList = new List<string>(animals);
Listing 1.
As you can see from Listing 1, the List<string> has an initial capacity set to 5 only. However, when more than 5 elements are added to the list, it automatically expands.
Как работает Быстрая сортировка
Быстрая сортировка чаще всего не сможет разделить массив на равные части. Это потому, что весь процесс зависит от того, как мы выбираем опорный элемент. Нам нужно выбрать опору так, чтобы она была примерно больше половины элементов и, следовательно, примерно меньше, чем другая половина элементов. Каким бы интуитивным ни казался этот процесс, это очень сложно сделать.
Подумайте об этом на мгновение — как бы вы выбрали адекватную опору для вашего массива? В истории быстрой сортировки было представлено много идей о том, как выбрать центральную точку — случайный выбор элемента, который не работает из-за того, что «дорогой» выбор случайного элемента не гарантирует хорошего выбора центральной точки; выбор элемента из середины; выбор медианы первого, среднего и последнего элемента; и еще более сложные рекурсивные формулы.
Самый простой подход — просто выбрать первый (или последний) элемент. По иронии судьбы, это приводит к быстрой сортировке на уже отсортированных (или почти отсортированных) массивах.
Именно так большинство людей выбирают реализацию быстрой сортировки, и, так как это просто и этот способ выбора опоры является очень эффективной операцией, и это именно то, что мы будем делать.
Теперь, когда мы выбрали опорный элемент — что нам с ним делать? Опять же, есть несколько способов сделать само разбиение. У нас будет «указатель» на нашу опору, указатель на «меньшие» элементы и указатель на «более крупные» элементы.
Цель состоит в том, чтобы переместить элементы так, чтобы все элементы, меньшие, чем опора, находились слева от него, а все более крупные элементы были справа от него. Меньшие и большие элементы не обязательно будут отсортированы, мы просто хотим, чтобы они находились на правильной стороне оси. Затем мы рекурсивно проходим левую и правую сторону оси.
Рассмотрим пошагово то, что мы планируем сделать, это поможет проиллюстрировать весь процесс. Пусть у нас будет следующий список.
19, 89,27,41,66,28,44,76,58,88,83,97,12,21,43
Выберем первый элемент как опору 19), а указатель на меньшие элементы (называемый «low») будет следующим элементом, указатель на более крупные элементы (называемый «high») станем последний элемент в списке.
19 | 89 (low), 27,41,66,28,44,76,58,88,83,97,12,21,43 (high)
Мы двигаемся в сторону high то есть влево, пока не найдем значение, которое ниже нашего опорного элемента.
19 | 89 (low),27,41,66,28,44,76,58,88,83,97,12,21 (high),43
- Теперь, когда наш элемент high указывает на элемент 21, то есть на значение меньше чем опорное значение, мы хотим найти значение в начале массива, с которым мы можем поменять его местами. Нет смысла менять местами значение, которое меньше, чем опорное значение, поэтому, если low указывает на меньший элемент, мы пытаемся найти тот, который будет больше.
- Мы перемещаем переменную low вправо, пока не найдем элемент больше, чем опорное значение. К счастью, low уже имеет значение 89.
- Мы меняем местами low и high:
19 | 21 (low),27,41,66,28,44,76,58,88,83,97,12,89 (high),43
- Сразу после этого мы перемещает high влево и low вправо (поскольку 21 и 89 теперь на своих местах)
- Опять же, мы двигаемся high влево, пока не достигнем значения, меньшего, чем опорное значение, и мы сразу находим — 12
- Теперь мы ищем значение больше, чем опорное значение, двигая low вправо, и находим такое значение 41
Этот процесс продолжается до тех пор, пока указатели low и high наконец не встретятся в одном элементе:
19 | 21,27,12,28 (low/high),44,66,76,58,88,83,97,12,89,43
Мы больше не используем это опорное значение, поэтому остается только поменять опорную точку и high, и мы закончили с этим рекурсивным шагом:
28,21,27,12,19,44,66,76,58,88,83,97,12,89,43
Как видите, мы достигли того, что все значения, меньшие 29, теперь слева от 29, а все значения больше 29 справа.
Затем алгоритм делает то же самое для коллекции 28,21,27,12,19 (левая сторона) и 66,76,58,88,83,97,12,89,43 (правая сторона). И так далее.
List.BinarySearch
Returns the zero-based index of the item in the sorted list. If the items is not found, returns a negative number. See MSDN for more info.
This List<T> method works only if the type T implements IComparable<T> or IComparable interface.
| list: | 1 3 4 6 7 9 |
|---|
| index: | 3 |
|---|
This BinarySearch method overload uses specified comparer.
| list: | 1 3 4 6 7 9 |
|---|
| index: | 3 |
|---|
This BinarySearch method overload uses specified comparer and search in specified range.
| list: | 1 3 4 6 7 9 |
|---|
| index: | 3 |
|---|
This example shows the case when the item was not found in the list. The result is negative number.
| list: | 1 3 4 6 7 9 |
|---|
| index: | -4 |
|---|
public class MyComparer : IComparer<int>
{
public int Compare(int x, int y) { return x.CompareTo(y); }
}
Двусвязные списки
Последнее обновление: 02.09.2016
Двусвязные списки также представляют последовательность связанных узлов, однако теперь каждый узел хранит ссылку на следующий и на предыдущий элементы.
Двунаправленность списка приходится учитывать при добавлении или удалении элемента,
так как кроме ссылки на следующий элемент надо устанавливать и ссылку на предыдущий. Но в то же время у нас появляется возможность обходить список как от первого к последнему
элементу, так и наоборот — от последнего к первому элементу. В остальном двусвязный список ни чем не будет отличаться от односвязного списка.
Для создания двусвязного списка вначале надо определить класс узла, который будет представлять элемент списка:
public class DoublyNode<T>
{
public DoublyNode(T data)
{
Data = data;
}
public T Data { get; set; }
public DoublyNode<T> Previous { get; set; }
public DoublyNode<T> Next { get; set; }
}
Далее определим сам класс списка:
using System.Collections.Generic;
using System.Collections;
namespace SimpleAlgorithmsApp
{
public class DoublyLinkedList<T> : IEnumerable<T> // двусвязный список
{
DoublyNode<T> head; // головной/первый элемент
DoublyNode<T> tail; // последний/хвостовой элемент
int count; // количество элементов в списке
// добавление элемента
public void Add(T data)
{
DoublyNode<T> node = new DoublyNode<T>(data);
if (head == null)
head = node;
else
{
tail.Next = node;
node.Previous = tail;
}
tail = node;
count++;
}
public void AddFirst(T data)
{
DoublyNode<T> node = new DoublyNode<T>(data);
DoublyNode<T> temp = head;
node.Next = temp;
head = node;
if (count == 0)
tail = head;
else
temp.Previous = node;
count++;
}
// удаление
public bool Remove(T data)
{
DoublyNode<T> current = head;
// поиск удаляемого узла
while (current != null)
{
if (current.Data.Equals(data))
{
break;
}
current = current.Next;
}
if(current!=null)
{
// если узел не последний
if(current.Next!=null)
{
current.Next.Previous = current.Previous;
}
else
{
// если последний, переустанавливаем tail
tail = current.Previous;
}
// если узел не первый
if(current.Previous!=null)
{
current.Previous.Next = current.Next;
}
else
{
// если первый, переустанавливаем head
head = current.Next;
}
count--;
return true;
}
return false;
}
public int Count { get { return count; } }
public bool IsEmpty { get { return count == 0; } }
public void Clear()
{
head = null;
tail = null;
count = 0;
}
public bool Contains(T data)
{
DoublyNode<T> current = head;
while (current != null)
{
if (current.Data.Equals(data))
return true;
current = current.Next;
}
return false;
}
IEnumerator IEnumerable.GetEnumerator()
{
return ((IEnumerable)this).GetEnumerator();
}
IEnumerator<T> IEnumerable<T>.GetEnumerator()
{
DoublyNode<T> current = head;
while (current != null)
{
yield return current.Data;
current = current.Next;
}
}
public IEnumerable<T> BackEnumerator()
{
DoublyNode<T> current = tail;
while (current != null)
{
yield return current.Data;
current = current.Previous;
}
}
}
}
По большому счету этот двусвязный список реализует те же действия, что и односвязный, разница заключается в необходимости установки свойства Previous для узлов списка.
В методе добавления , если в списке уже есть элементы, то у добавляемого узла свойство указывает на узел, который до этого
хранился в переменной tail:
if (head == null)
head = node;
else
{
tail.Next = node;
node.Previous = tail;
}
tail = node;
Аналогично в методе добавлении в начало списка для головного элемента свойство Previous начинает указывать на новый элемент, а новый
элемент, таким образом, становиться первым элементом в списке.
При удалении вначале необходимо найти удаляемый элемент. Затем в общем случае надо переустановить две ссылки:
current.Next.Previous = current.Previous; current.Previous.Next = current.Next;
Если удаляются первый и последний элемент, соответственно надо переустановить переменные head и tail.
И также в отличие от односвязной реализации здесь добавлен метод для перебора элементов с конца.
Применение списка:
DoublyLinkedList<string> linkedList = new DoublyLinkedList<string>();
// добавление элементов
linkedList.Add("Bob");
linkedList.Add("Bill");
linkedList.Add("Tom");
linkedList.AddFirst("Kate");
foreach (var item in linkedList)
{
Console.WriteLine(item);
}
// удаление
linkedList.Remove("Bill");
// перебор с последнего элемента
foreach (var t in linkedList.BackEnumerator())
{
Console.WriteLine(t);
}
НазадВперед