Двоичный код в текст
Содержание:
- Арифметические действия в шестнадцатеричной системе счисления
- Что мы узнали?
- Описание числа 1011101
- Перевод чисел из десятичной системы счисления в другую систему счисления
- Как отличить двоичное, шестнадцатеричное и десятичное написание друг от друга
- Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
- Перевод из восьмеричной системы в двоичную
- Побитовые операции над строками
- Перевод чисел из десятичной системы счисления в другую систему счисления
- Один миллион одиннадцать тысяч сто один
- Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
- ASCII и HTML
- Побитовые операции с цифрами: нужно переводить в двоичную систему сами цифры или брать двоичные значения ASCII каждого символа?
- Об этой статье
- Для кого эта статья
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.
Рис. 2. Таблица сложения шестнадцатеричных чисел
Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
Рис. 3. Таблица умножения шестнадцатеричных чисел
Например, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.
Что мы узнали?
В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел
Описание числа 1011101
Рациональное
семизначное
число 1011101
является составным числом.
Сумма и произведение цифр числа: 5, 0.
16 — количество делителей.
Обратным числом является 9.890208792197811e-7.
Число 1011101 можно представить произведением простых чисел: 7 * 13 * 41 * 271.
Другие системы счисления:
двоичная система: 11110110110110011101, троичная система: 1220100222012, восьмеричная система: 3666635, шестнадцатеричная система: F6D9D.
В числе байт 1011101 содержится 987 килобайтов 413 байтов информации.
Азбука Морзе для числа 1011101: .—- —— .—- .—- .—- —— .—-
Синус числа 1011101: -0.9847, косинус числа 1011101: -0.1743, тангенс числа 1011101: 5.6491.
У числа есть натуральный логарифм: 13.8266.
Логарифм десятичный числа: 6.0048.
Если извлечь квадратный корень, получится 1005.5352, а если кубический корень — 100.3687
Возведение числа 1011101 в квадрат: 1.0223e+12.
1 неделя 4 дня 16 часов 51 минута 41 секунда представляет из себя число секунд 1011101.
Цифра 5 — это нумерологическое значение этого числа.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Source: matworld.ru
Как отличить двоичное, шестнадцатеричное и десятичное написание друг от друга
Конкретные нотации могут различаться в зависимости от языка программирования или используемой программы (printf, printf, xxd, hexdump и так далее), но обычно используются следующие правила:
По умолчанию целочисленный литерал (число) — это десятичное целое число.
Для обозначения двоичного целочисленного литерала перед ним используется 0b или 0B (ноль B). Иногда буква b ставится позади числа.
Для обозначения восьмеричного целочисленного литерала, перед ним используется (ноль).
А для обозначения шестнадцатеричного целочисленного литерала, перед ним используется 0x или 0X (ноль X).
В Radare2 можно увидеть такую запись:
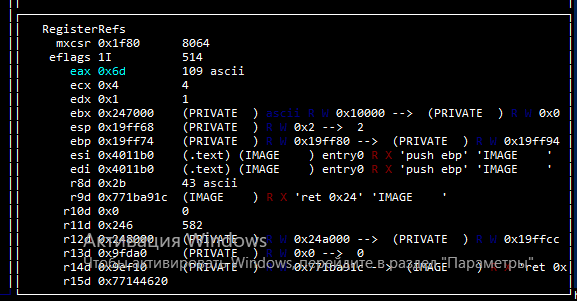
Обратите внимание на переменную eax, значение которой равно 0x6d, а затем дано пояснение 109 ascii. То есть в шестнадцатеричном виде значение переменной eax равно 0x6d, в десятеричном это 109 что соответствует символу m.
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
|
Двоичная СС |
Восьмеричная СС |
|
000 |
|
|
001 |
1 |
|
010 |
2 |
|
011 |
3 |
|
100 |
4 |
|
101 |
5 |
|
110 |
6 |
|
111 |
7 |
Пример перевода из шестнадцатеричной системы в двоичную: A5E16 = 1010 0101 1110 = 1010010111102
Пример перевода из двоичной системы в шестнадцатеричную: 1111001112 = 0001 1110 0111 = 1E716
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.
Автоматический перевод. Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
Перевод из восьмеричной системы в двоичную
Способ 1:
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Возьмем число 438.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 1000112
Способ 2:
Используем таблицу триад:
| Цифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
3518 = (011) (101) (001) = 0111010012 = 111010012
Побитовые операции над строками
К побитовым операторам относятся:
- И (AND)
- Отрицание
- Побитовое (включающее) ИЛИ (OR)
- Побитовое ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
- Побитовый сдвиг (влево и вправо)
Если вспомнить школьный/ВУЗовский курс логики, то там такие операции выполняются с нулями и единицами. То есть их можно выполнить с бинарными данными, например, с двоичными числами.
В языках программирования можно делать побитовые операции с десятичными числами, например Побитовое ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) в PHP:
echo 8 ^ 5;
Выведет:
13
Дело в том, что числа будут автоматически переведены в двоичный вид и операция будет выполнена уже над двоичными числами.
Пример выше можно проверить вручную. Операция ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) означает, что устанавливаются только те биты, которые установлены либо только в $a, либо только в $b, но не в обоих одновременно.
8 и 5 в двоичном виде это соответственно 1000 и 101, можно также из записать так: 1000 и 0101.
Итак:
- смотрим первый бит — в первом числе он установлен (1) а во втором — не установлен (0), следовательно, в конечном числе он будет установлен (1)
- смотрим второй бит — в первом числе он не установлен (0) а во втором — установлен (1), следовательно, в конечном числе он будет установлен (1)
- смотрим третий бит — в первом числе он не установлен (0) и во втором — не установлен (0), следовательно, в конечном числе он не будет установлен ()
- смотрим четвёртый бит — в первом числе он не установлен (0) а во втором — установлен (1), следовательно, в конечном числе он будет установлен (1)
Получаем конечное число: 1101
Проверяем:
rax2 1101d 13
То есть в PHP операция проделана правильно, даже не смотря на то, что мы указали не двоичные числа, а десятичные.
Когда говорят о побитовых операциях со строками, то имеют в виду, что используется ASCII код символа (который затем переводиться в двоичный вид). После выполнения требуемой операции, выполняется обратное преобразование — число переводиться в ASCII символ.
Кстати, про ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) — у этой операции есть интересное свойство:
- Как мы уже видели, 8 ^ 5 = 13
- При этом: 13 ^ 5 = 8
- И: 8 ^ 13 = 5
То есть можно взять строки и выполнить между ними операцию XOR. В результате получиться бессмысленный набор символов. Затем если между этой бессмысленной строкой и любой из первоначальных строк вновь выполнить операцию XOR, то получиться вторая начальная строка.
На этом основано простейшее симметричное шифрование: исходный текст шифруется паролем с помощью XOR. То есть с первым символом текста и первыми символом пароля делается операция XOR, затем со вторым символом шифруемого текста и вторым символом пароля делается операция XOR и так далее, пока шифруемый текст не кончится. Поскольку пароль обычно короче шифруемого текста, то когда он заканчивается, вновь выполняется переход к первому символу пароля и так далее много раз.
В результате получается бессмысленный набор символов, которые можно расшифровать этим же паролем выполняя эту же операцию XOR.
Правда, зашифрованные таким образом тексты часто приводятся для тренировки в литературе по взлому шифров: если текст достаточно длинный, то с помощью статистического анализа того, как часто в нём встречаются символы и сравнивая эту частотность с естественной частотностью букв в языке, сначала вычисляют длину пароля, а затем и сам пароль. То есть это крайне ненадёжный шифр.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Один миллион одиннадцать тысяч сто один
| Сумма цифр | |
| Произведение цифр | |
| Произведение цифр (без учета ноля) | |
| Количество цифр в числе | (семизначное число) |
| Все делители числа | 1, 7, 13, 41, 91, 271, 287, 533, 1897, 3523, 3731, 11111, 24661, 77777, 144443, 1011101 |
| Наибольший делитель из ряда степеней двойки | |
| Количество делителей | |
| Сумма делителей | |
| Простое число? | Нет |
|
Полупростое число? |
Нет |
| Обратное число | 9.890208792197811e-7 |
| Индо-арабское написание | ١٠١١١٠١ |
| Азбука морзе | .—- —— .—- .—- .—- —— .—- |
|
Факторизация |
* * * |
| Двоичный вид | 11110110110110011101 |
| Троичный вид | |
| Восьмеричный вид | |
| Шестнадцатеричный вид (HEX) | F6D9D |
| Перевод из байтов | килобайтов байтов |
| Цвет | RGB(15, 109, 157) или #0F6D9D |
| Наибольшая цифра в числе(возможное основание) | (2, двоичный вид) |
| Перевод двоичной записи в десятичную | |
| Число Фибоначчи? | Нет |
|
Нумерологическое значение |
свобода, движение, разнообразие, приключения, путешествия, риск, опасность, страх |
| Синус числа | -0.9846907168190582 |
| Косинус числа | -0.17431061990128247 |
| Тангенс числа | 5.649057512254384 |
| Натуральный логарифм | 13.82655039410086 |
| Десятичный логарифм | 6.004794539915235 |
| Квадратный корень | 1005.5351808862781 |
| Кубический корень | 100.36867246911392 |
| Квадрат числа | |
| Перевод из секунд | неделя дня часов минута секунда |
| Дата по UNIX-времени | Mon, Jan 16:51:41 GMT |
| MD5 | 55495438a3d6b618080c5ce0f8c34105 |
| SHA1 | 8b5bdcc9cb91a4240c15d0b5d24fce118314eb21 |
| Base64 | MTAxMTEwMQ== |
| QR-код числа 1011101 |
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 |
Тогда число 6372 можно представить в следующем виде:
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
В общем случае формулу можно представить в следующем виде:
Цn·sn+Цn-1·sn-1+…+Ц1·s1+Ц·s+Д-1·s-1+Д-2·s-2+…+Д-k·s-k
(1)
где Цn-целое число в позиции n, Д-k— дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
ASCII и HTML
Если в HTML коде перед десятичным кодом ASCII символа поставить &#, то веб-браузер отобразит этот символ.
К примеру, если использовать ', то веб-браузер покажет ‘ (одинарную кавычку). Некоторые преобразователи строк внутри веб-приложения также могут конвертировать написание символов &#XX в их ASCII представления. Поэтому безобидная запись ' внутри веб-приложения может превратиться в одинарную кавычку, которая может нарушить SQL запрос.
Аналогично можно использовать &#x, после которой нужно указать код символа в шестнадцатеричной системе, например, ' также покажет кавычку. Для разделения символов друг от друга, используйте точку с запятой, например, 'hi'
Многие программы понимают шестнадцатеричную запись, правда вид записи может различаться от конкретной программы и языка программирования.
В JavaScript шестнадцатеричные строки записываются в виде экранированной последовательности:
<script>
alert ("\x27\x68\x69\x27")
</script>
Можно записать код символов в восьмеричной системе счисления:
<script>
alert ("\47\150\151\47")
</script>
Аналогично Bash понимает такие строки:
echo -e "\x27\x68\x69\x27" 'hi'
И PHP их обрабатывает верно:
<?php echo "\x27\x68\x69\x27";
Также выведет:
'hi'
Побитовые операции с цифрами: нужно переводить в двоичную систему сами цифры или брать двоичные значения ASCII каждого символа?
Допустим, мы хотим сделать побитовую операцию 5 OR 7. Какой будет результат? Микропроцессор не работает ни с числами в десятичной системе, ни с ASCII строками — микропроцессор работает только двоичными числами.
То есть возникает вопрос:
1. Это числа?
2. Это ASCII строки?
Рассмотрим оба эти варианта, чтобы понять, насколько они различаются.
1.
5 и 7 — это числа
Число 5 в двоичной системе это 101, а число 7 в двоичной системе это 111.
В результате выполнения
101 OR 111
Будет получено 111. То есть результатом данной операции является число 7.
2.
5 и 7 — это ASCII строки
Смотрим таблицу ASCII символов, там цифре 5 соответствует код 00110101, а цифре 7 соответствует код 00110111. Делаем побитовую операцию OR между ними:
00110101 OR 00110111
Получаем: 110111, что в таблице ASCII символов также соответствует символу «7».
Итак, в принципе, можно напрямую переводить данные цифры в их двоичные значения, либо можно использовать двоичные значения их символов. Самое главное, придерживаться одной и той же схемы и преобразовывать с учётом выбранного пути. Ведь если вы делаете логическую операцию (например OR), с ASCII значением, а затем начинаете толковать полученный результат как число, то такое число (в нашем примере), будет равно 110111 = 55 (в десятичной системе). Или наоборот, вы сделали побитовую операцию между 101 OR 111, а затем полученный результат 111 начинаете трактовать как ASCII код символа — то тогда вместо числа вы получите управляющий символ «звуковой сигнал: звонок».
Об этой статье
Соавтор(ы):
Штатный редактор wikiHow
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту. wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества. Количество просмотров этой статьи: 90 758.
Категории: Школа
English:Convert Binary to Hexadecimal
Español:convertir un binario en hexadecimal
Italiano:Passare da Sistema Binario a Esadecimale
Português:Converter Números Binários Para Hexadecimais
Français:convertir du binaire en hexadécimal
Bahasa Indonesia:Mengonversikan Bilangan Biner Menjadi Heksadesimal
Nederlands:Binair omzetten naar hexadecimaal
日本語:二進法を十六進法に変換する
ไทย:แปลงเลขฐานสองเป็นเลขฐานสิบหก
العربية:التحويل من النظام الثنائي إلى النظام الستة عشري
한국어:2진수를 16진수로 바꾸는 법
中文:把二进制转换为十六进制
हिन्दी:बाइनरी को हेक्साडेसिमल में बदलें (Convert Binary to Hexadecimal)
Печать
Для кого эта статья
Вам абсолютно точно нужно понимать суть ASCII кодирования символов, а также шестнадцатеричную запись строк если вы:
- программируете
- занимаетесь отладкой и обратным инжинирингом программ
- выполняете тесты на проникновение (шестнадцатеричная и другие варианты записи широко используются для обхода файловых файерволов, фильтров и других систем защиты веб-приложений)
Примечание: правда, я исхожу из того, что вы знаете что такое:
- система счисления
- десятичная, шестнадцатеричная, двоичная система счисления
- умеете конвертировать числа между этими системами счисления
- логические операции И, ИЛИ
По идее, это охватывается базовым курсом информатики и логики на любых специальностях в ВУЗе (некоторые учат это уже в школе) и это должен знать каждый — поэтому я не будут на этом останавливаться. Если вы не знаете даже этого, то прежде чем читать эту заметку, начните с ликвидации ваших более базовых пробелов про системы счисления.