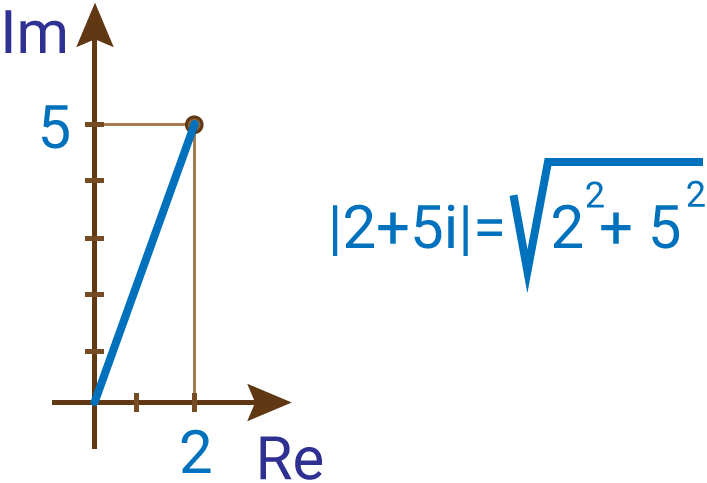Math.abs 方法

Utils functions #

Function	Description
math.clone(x)	Clone an object.
math.hasNumericValue(x)	Test whether a value is an numeric value.
math.isInteger(x)	Test whether a value is an integer number.
math.isNaN(x)	Test whether a value is NaN (not a number).
math.isNegative(x)	Test whether a value is negative: smaller than zero.
math.isNumeric(x)	Test whether a value is an numeric value.
math.isPositive(x)	Test whether a value is positive: larger than zero.
math.isPrime(x)	Test whether a value is prime: has no divisors other than itself and one.
math.isZero(x)	Test whether a value is zero.
math.numeric(x)	Convert a numeric input to a specific numeric type: number, BigNumber, or Fraction.
math.typeOf(x)	Determine the type of a variable.

API #

All relevant functions in math.js support Matrices and Arrays. Functions like and , handle matrices element wise. There is a set of functions specifically for creating or manipulating matrices, such as:

• Functions like and , , , and to create a matrix.
• Functions like and to get or replace a part of a matrix
• Functions like and to manipulate matrices.

A full list of matrix functions is available on the .

Two types of matrix classes are available in math.js, for storage of dense and sparse matrices. Although they contain public functions documented as follows, using the following API directly is not recommended. Prefer using the functions in the “math” namespace wherever possible.

• DenseMatrix
• SparseMatrix

Тригонометрические функции

math.sin(x)

Возвращает синус угла x значение которого задано в радианах.

math.cos(x)

Возвращает косинус угла x значение которого задано в радианах.

math.tan(x)

Возвращает тангенс угла x значение которого задано в радианах.

При определенных значениях углов тангенс должен быть равен либо \(-\infty\) либо \(+\infty\), скажем \(\tan (3\pi/2) = +\infty\), a \(\tan (-\pi/2) = -\infty\), но вместо этого мы получаем либо очень большие либо очень маленькие значения типа float:

math.asin(x)

Возвращает арксинус значения x, т.е. такое значение угла y (выраженного в радианах) при котором .

math.acos(x)

Возвращает арккосинус значения x, т.е. возвращает такое значение угла y (выраженного в радианах) при котором .

math.atan(x)

Возвращает арктангенс значения x, т.е. возвращает такое значение угла y (выраженного в радианах) при котором .

math.atan2(y, x)

Возвращает арктангенс значения x/y, т.е. возвращает такое значение угла z (выраженного в радианах) при котором .

Однако, данная функция, в отличие от функции , способна вычислить правильный квадрвнт в котором должно находиться значение результата. Это возможно благодаря тому, что функция принимает два аргумента – это координаты точки, которая является концом отрезка начатого в начале координат

Сам по себе, угол между этим отрезком и положительным направлением оси абцисс не несет информации о том где располагается конец этого отрезка, что приводит к одинаковому значению арктангенса, для разных отрезков, но функция позволяет избежать этого, что бывает очень важно в целом ряде задач:

math.hypot(x, y)

Вычисляет значение гипотенузы по заданным значениям катетов x и y. Данная функция равносильна команде .

1.2 Алгебраические функции в Java

В большинстве случаев программисту с головой хватает школьной математики: даже синусы и косинусы в коде можно встретить очень редко. Чаще всего они нужны при работе с играми, картами или игровыми движками. 90% программистов с этим никогда не сталкиваются.

Но, кроме геометрии, программистам иногда приходится использовать и алгебраические функции. И, конечно же, класс содержит самые распространенные из них:

Метод	Описание
	квадратный корень из
	кубический корень из
	возведение в степень:
	экспонента:
	натуральный логарифм :
	десятичный логарифм :
	натуральный логарифм :

Если вам нужен квадратный или кубический корень из числа, для этого есть функции и .

Корень из двух можно вычислить так:

Если вы хотите получить корень более высокой степени, воспользуйтесь функцией возведения в степень: в степени — это и будет корень четвертой степени, и т.д.

Для работы с логарифмами и экспонентами есть функции – натуральный логарифм и — экспонента. Для вычисления десятичного логарифма есть функция .

Если вам нужен логарифм числа по основанию , воспользуйтесь простой формулой:

Полезные функции

Последние две функции и могут быть вам полезны, если вы проводите вычисления при очень маленьких значениях .

При сложении очень маленьких и очень больших переменных часто может возникнуть ситуация, когда очень маленькое значение просто игнорируется (отбрасывается) как незначащее. Это, собственно, и будет происходить, если использовать функции и . Поэтому программисты придумали функции, которые возвращают только ту самую «маленькую значащую часть»

Пример:

Вы хотите посчитать натуральный логарифм от , где равен . Вы просто не сможете передать это число в функцию , т.к. если сложить и , получится . — настолько маленькое число, что будет отброшено полностью при сложении чисел.

А т.к. в математике часто приходится вычислять при числах, близких к , программисты придумали способ обойти эту проблему: передать в функцию не само число, а только его отличие от .

Function transforms #

It is possible to preprocess function arguments and post process a functions
return value by writing a transform for the function. A transform is a
function wrapping around a function to be transformed or completely replaces
a function.

For example, the functions for math.js use zero-based matrix indices (as is
common in programing languages), but the expression parser uses one-based
indices. To enable this, all functions dealing with indices have a transform,
which changes input from one-based to zero-based, and transforms output (and
error message) from zero-based to one-based.

To create a transform for a function, the transform function must be attached
to the function as property :

Functions with a transform must be imported in the namespace, as they
need to be processed at compile time. They are not supported when passed via a
scope at evaluation time.

User-Defined Units #

You can add your own units to Math.js using the function. The following example defines a new unit , then uses the user-defined unit in a calculation:

If you cannot express the new unit in terms of any existing unit, then the second argument can be omitted. In this case, a new base unit is created:

The second argument to can also be a configuration object consisting of the following properties:

• definition A or which defines the user-defined unit in terms of existing built-in or user-defined units. If omitted, a new base unit is created.
• prefixes A indicating which prefixes math.js should use with the new unit. Possible values are , , , , or . Default is .
• offset A value applied when converting to the unit. This is very helpful for temperature scales that do not share a zero with the absolute temperature scale. For example, if we were defining fahrenheit for the first time, we would use:
• aliases An array of strings to alias the new unit. Example:
• baseName A that specifies the name of the new dimension in case one needs to be created. Every unit in math.js has a dimension: length, time, velocity, etc. If the unit’s doesn’t match any existing dimension, or it is a new base unit, then will create a new dimension with the name and assign it to the new unit. The default is to append to the unit’s name. If the unit already matches an existing dimension, this option has no effect.

An optional object can also be supplied as the last argument to . Currently only the option is supported:

Base units created without specifying a definition cannot be overridden.

Multiple units can defined using a single call to by passing an object map as the first argument, where each key in the object is the name of a new unit and the value is either a string defining the unit, or an object with the configuration properties listed above. If the value is an empty string or an object lacking a definition property, a new base unit is created.

For example:

Return Value

returns the created unit, or, when multiple units are created, the last unit created. Since is also compatible with the expression parser, this allows you to do things like this:

Trigonometry functions #

Function	Description
math.acos(x)	Calculate the inverse cosine of a value.
math.acosh(x)	Calculate the hyperbolic arccos of a value, defined as .
math.acot(x)	Calculate the inverse cotangent of a value, defined as .
math.acoth(x)	Calculate the hyperbolic arccotangent of a value, defined as .
math.acsc(x)	Calculate the inverse cosecant of a value, defined as .
math.acsch(x)	Calculate the hyperbolic arccosecant of a value, defined as .
math.asec(x)	Calculate the inverse secant of a value.
math.asech(x)	Calculate the hyperbolic arcsecant of a value, defined as .
math.asin(x)	Calculate the inverse sine of a value.
math.asinh(x)	Calculate the hyperbolic arcsine of a value, defined as .
math.atan(x)	Calculate the inverse tangent of a value.
math.atan2(y, x)	Calculate the inverse tangent function with two arguments, y/x.
math.atanh(x)	Calculate the hyperbolic arctangent of a value, defined as .
math.cos(x)	Calculate the cosine of a value.
math.cosh(x)	Calculate the hyperbolic cosine of a value, defined as .
math.cot(x)	Calculate the cotangent of a value.
math.coth(x)	Calculate the hyperbolic cotangent of a value, defined as .
math.csc(x)	Calculate the cosecant of a value, defined as .
math.csch(x)	Calculate the hyperbolic cosecant of a value, defined as .
math.sec(x)	Calculate the secant of a value, defined as .
math.sech(x)	Calculate the hyperbolic secant of a value, defined as .
math.sin(x)	Calculate the sine of a value.
math.sinh(x)	Calculate the hyperbolic sine of a value, defined as .
math.tan(x)	Calculate the tangent of a value.
math.tanh(x)	Calculate the hyperbolic tangent of a value, defined as .

Getting or replacing subsets #

Subsets of a matrix can be retrieved or replaced using the function .
Matrices have a function, which is applied to the matrix itself:
. For both matrices and arrays,
the static function can be used.
When parameter is provided, the function will replace a subset
in the matrix, and if not, a subset of the matrix will be returned.

A subset can be defined using an . An contains a single value
or a set of values for each dimension of a matrix. An can be
created using the function .
Matrix indexes in math.js are zero-based, like most programming languages
including JavaScript itself.

Note that mathematical applications like Matlab and Octave work differently,
as they use one-based indexes.

Custom HTML, LaTeX and string output #

All expression nodes have a method and to output an expression respectively in HTML or LaTex format or as regular text .
The functions , and accept an argument to customise output. This object is of the following form:

Parenthesis

The option changes the way parentheses are used in the output. There are three options available:

• Keep the parentheses from the input and display them as is. This is the default.
• Only display parentheses that are necessary. Mathjs tries to get rid of as much parentheses as possible.
• Display all parentheses that are given by the structure of the node tree. This makes the output precedence unambiguous.

There’s two ways of passing callbacks:

1. Pass an object that maps function names to callbacks. Those callbacks will be used for FunctionNodes with
   functions of that name.
2. Pass a function to . This function will then be used for every node.

Handler

You can provide the and functions of an expression with your own custom handlers that override the internal behaviour. This is especially useful to provide LaTeX/string output for your own custom functions. This can be done in two ways:

1. Pass an object that maps function names to callbacks. Those callbacks will be used for FunctionNodes that contain functions with that name.
2. Pass a callback directly. This callback will run for every node, so you can replace the output of anything you like.

A callback function has the following form:

Where is the object passed to //. Don’t forget to pass this on to the child nodes, and is a reference to the current node.

If a callback returns nothing, the standard output will be used. If your callback returns a string, this string will be used.

Although the following examples use , it works for and in the same way

Examples for option 2:

Another example in conjunction with custom functions:

Implicit multiplication

You can change the way that implicit multiplication is converted to a string or LaTeX. The two options are , to not show a multiplication operator for implicit multiplication and to show it.

Example:

Math Object Methods

Method	Description
abs(x)	Returns the absolute value of x
acos(x)	Returns the arccosine of x, in radians
acosh(x)	Returns the hyperbolic arccosine of x
asin(x)	Returns the arcsine of x, in radians
asinh(x)	Returns the hyperbolic arcsine of x
atan(x)	Returns the arctangent of x as a numeric value between -PI/2 and PI/2 radians
atan2(y, x)	Returns the arctangent of the quotient of its arguments
atanh(x)	Returns the hyperbolic arctangent of x
cbrt(x)	Returns the cubic root of x
ceil(x)	Returns x, rounded upwards to the nearest integer
cos(x)	Returns the cosine of x (x is in radians)
cosh(x)	Returns the hyperbolic cosine of x
exp(x)	Returns the value of Ex
floor(x)	Returns x, rounded downwards to the nearest integer
log(x)	Returns the natural logarithm (base E) of x
max(x, y, z, …, n)	Returns the number with the highest value
min(x, y, z, …, n)	Returns the number with the lowest value
pow(x, y)	Returns the value of x to the power of y
random()	Returns a random number between 0 and 1
round(x)	Rounds x to the nearest integer
sin(x)	Returns the sine of x (x is in radians)
sinh(x)	Returns the hyperbolic sine of x
sqrt(x)	Returns the square root of x
tan(x)	Returns the tangent of an angle
tanh(x)	Returns the hyperbolic tangent of a number
trunc(x)	Returns the integer part of a number (x)

Nodes #

math.js has the following types of nodes. All nodes are available at the
namespace .

AccessorNode

Construction:

Properties:

• (read-only) The function or method name. Returns an empty string when undefined.

Examples:

Construction:

Properties:

items: Node[]

Examples:

AssignmentNode

Construction:

Properties:

• (read-only) The function or method name. Returns an empty string when undefined.

Examples:

BlockNode

A is created when parsing a multi line expression like or
. Evaluating a returns a . The results can be
retrieved via or , which contains
an with the results of the visible lines (i.e. lines not ending with
a semicolon).

Construction:

Properties:

blocks: Array.

Examples:

Construction:

Properties:

Examples:

Construction:

Properties:

value: *

Examples:

Construction:

Properties:

Examples:

Construction:

Properties:

• (read-only) The object or function name which to invoke.

Examples:

IndexNode

Construction:

Each dimension can be a single value, a range, or a property. The values of
indices are one-based, including range end.

An optional property can be provided describing whether this index
was written using dot notation like , or using bracket notation
like . Default value is . This information is used when
stringifying the IndexNode.

Properties:

Examples:

Construction:

Properties:

properties: Object.

Examples:

OperatorNode

Construction:

Additional methods:

• Returns true when the contains exactly one argument,
  like with a unary minus:

• Returns true when the contains exactly two arguments,
  like with most regular operators:

Properties:

Examples:

Construction:

Properties:

content: Node

Examples:

Construction:

Properties:

Examples:

RelationalNode

Construction:

is an array of strings, each of which may be ‘smaller’, ‘larger’, ‘smallerEq’, ‘largerEq’, ‘equal’, or ‘unequal’. The array must contain exactly one fewer item than .

Properties:

A efficiently represents a chained conditional expression with two or more comparison operators, such as . The expression is equivalent to , except that is evaluated only once, and evaluation stops (is “short-circuited”) once any condition tests false. Operators that are subject to chaining are , , , , , and . For backward compatibility, will return an if only a single conditional is present (such as ).

Examples:

Probability functions #

Function	Description
math.combinations(n, k)	Compute the number of ways of picking unordered outcomes from possibilities.
math.combinationsWithRep(n, k)	Compute the number of ways of picking unordered outcomes from possibilities, allowing individual outcomes to be repeated more than once.
math.factorial(n)	Compute the factorial of a value Factorial only supports an integer value as argument.
math.gamma(n)	Compute the gamma function of a value using Lanczos approximation for small values, and an extended Stirling approximation for large values.
math.kldivergence(x, y)	Calculate the Kullback-Leibler (KL) divergence between two distributions.
math.multinomial(a)	Multinomial Coefficients compute the number of ways of picking a1, a2, .
math.permutations(n )	Compute the number of ways of obtaining an ordered subset of elements from a set of elements.
math.pickRandom(array)	Random pick one or more values from a one dimensional array.
math.random()	Return a random number larger or equal to and smaller than using a uniform distribution.
math.randomInt()	Return a random integer number larger or equal to and smaller than using a uniform distribution.

Data types #

The expression parser supports booleans, numbers, complex numbers, units,
strings, matrices, and objects.

Booleans

Booleans and can be used in expressions.

Booleans can be converted to numbers and strings and vice versa using the
functions and , and .

Numbers

The most important and basic data type in math.js are numbers. Numbers use a
point as decimal mark. Numbers can be entered with exponential notation.
Examples:

A number can be converted to a string and vice versa using the functions
and .

Math.js uses regular JavaScript numbers, which are floating points with a
limited precision and limited range. The limitations are described in detail
on the page Numbers.

When doing calculations with floats, one can very easily get round-off errors:

When outputting results, the function can be used to hide
these round-off errors when outputting results for the user:

BigNumbers

Math.js supports BigNumbers for calculations with an arbitrary precision.
The pros and cons of Number and BigNumber are explained in detail on the page
Numbers.

BigNumbers are slower but have a higher precision. Calculations with big
numbers are supported only by arithmetic functions.

BigNumbers can be created using the function:

The default number type of the expression parser can be changed at instantiation
of math.js. The expression parser parses numbers as BigNumber by default:

BigNumbers can be converted to numbers and vice versa using the functions
and . When converting a BigNumber to a Number, the high
precision of the BigNumber will be lost. When a BigNumber is too large to be represented
as Number, it will be initialized as .

Complex numbers

Complex numbers can be created using the imaginary unit , which is defined
as . Complex numbers have a real and complex part, which can be
retrieved using the functions and .

Math.js does not automatically convert complex numbers with an imaginary part
of zero to numbers. They can be converted to a number using the function
.

Units

math.js supports units. Units can be used in the arithmetic operations
add, subtract, multiply, divide, and exponentiation.
Units can also be converted from one to another.
An overview of all available units can be found on the page
Units.

Units can be converted using the operator or .

Strings

Strings are enclosed by double quotes “ or single quotes ‘. Strings can be concatenated using the
function (not by adding them using like in JavaScript). Parts of
a string can be retrieved or replaced by using indexes. Strings can be converted
to a number using function , and numbers can be converted to a string
using function .

When setting the value of a character in a string, the character that has been
set is returned. Likewise, when a range of characters is set, that range of
characters is returned.

Strings can be used in the function, to parse expressions inside
the expression parser:

Matrices

Matrices can be created by entering a series of values between square brackets,
elements are separated by a comma .
A matrix like will create a vector, a 1-dimensional matrix with
size . To create a multi-dimensional matrix, matrices can be nested into
each other. For easier creation of two-dimensional matrices, a semicolon
can be used to separate rows in a matrix.

Another way to create filled matrices is using the functions , ,
, and .

A subset can be retrieved from a matrix using indexes and a subset of a matrix
can be replaced by using indexes. Indexes are enclosed in square brackets, and
contain a number or a range for each of the matrix dimensions. A range can have
its start and/or end undefined. When the start is undefined, the range will start
at 1, when the end is undefined, the range will end at the end of the matrix.
There is a context variable available as well to denote the end of the
matrix.

IMPORTANT: matrix indexes and ranges work differently from the math.js indexes
in JavaScript: They are one-based with an included upper-bound, similar to most
math applications.

Creation #

A matrix can be created from an array using the function . The
provided array can contain nested arrays in order to create a multi-dimensional matrix. When called without arguments, an empty matrix will be
created.

Math.js supports regular Arrays. Multiple dimensions can be created
by nesting Arrays in each other.

Matrices can contain different types of values: numbers, complex numbers,
units, or strings. Different types can be mixed together in a single matrix.

There are a number of functions to create a matrix with a specific size and
content: , , .

The functions , , and also accept a single array
or matrix containing the dimensions for the matrix. When the input is an Array,
the functions will output an Array. When the input is a Matrix, the output will
be a Matrix. Note that in case of numbers as arguments, the output is
determined by the option as discussed in section
.

Ranges can be created using the function . The function is
called with parameters start and end, and optionally a parameter step.
The start of the range is included, the end of the range is excluded.

Description

The java.lang.Math.pow(double a, double b) returns the value of the first argument raised to the power of the second argument. Special cases −

• If the second argument is positive or negative zero, then the
  result is 1.0.

• If the second argument is 1.0, then the result is the same as the
  first argument.

• If the second argument is NaN, then the result is NaN.

• If the first argument is NaN and the second argument is nonzero,
  then the result is NaN.

• If

  • the absolute value of the first argument is greater than 1 and the second argument is positive infinity, or

  • the absolute value of the first argument is less than 1 and the second argument is negative infinity,

then the result is positive infinity.

If

• the absolute value of the first argument is greater than 1 and the second argument is negative infinity, or

• the absolute value of the first argument is less than 1 and the second argument is positive infinity,

then the result is positive zero.

If the absolute value of the first argument equals 1 and the second argument is infinite, then the result is NaN.

If

• the first argument is positive zero and the second argument is greater than zero, or

• the first argument is positive infinity and the second argument is less than zero,

then the result is positive zero.

If

• the first argument is positive zero and the second argument is less than zero, or

• the first argument is positive infinity and the second argument is greater than zero,

then the result is positive infinity.

If

• the first argument is negative zero and the second argument is greater than zero but not a finite odd integer, or

• the first argument is negative infinity and the second argument is less than zero but not a finite odd integer,

then the result is positive zero.

If

• the first argument is negative zero and the second argument is a positive finite odd integer, or

• the first argument is negative infinity and the second argument is a negative finite odd integer,

then the result is negative zero.

If

• the first argument is negative zero and the second argument is less than zero but not a finite odd integer, or

• the first argument is negative infinity and the second argument is greater than zero but not a finite odd integer,

then the result is positive infinity.

If

• the first argument is negative zero and the second argument is a negative finite odd integer, or

• the first argument is negative infinity and the second argument is a positive finite odd integer,

then the result is negative infinity.

If the first argument is finite and less than zero

• if the second argument is a finite even integer, the result is equal to the result of raising the absolute value of the first argument to the power of the second argument

• if the second argument is a finite odd integer, the result is equal to the negative of the result of raising the absolute value of the first argument to the power of the second argument

• if the second argument is finite and not an integer, then the result is NaN.

If both arguments are integers, then the result is exactly equal to the mathematical result of raising the first argument to the power of the second argument if that result can in fact be represented exactly as a value.

(In the foregoing descriptions, a floating-point value is considered to be an integer if and only if it is finite and a fixed point of the method ceil or, equivalently, a fixed point of the method floor. A value is a fixed point of a one-argument method if and only if the result of applying the method to the value is equal to the value.)

The computed result must be within 1 ULP of the exact result. Results must be semi-monotonic.

Set functions #

Function	Description
math.setCartesian(set1, set2)	Create the cartesian product of two (multi)sets.
math.setDifference(set1, set2)	Create the difference of two (multi)sets: every element of set1, that is not the element of set2.
math.setDistinct(set)	Collect the distinct elements of a multiset.
math.setIntersect(set1, set2)	Create the intersection of two (multi)sets.
math.setIsSubset(set1, set2)	Check whether a (multi)set is a subset of another (multi)set.
math.setMultiplicity(element, set)	Count the multiplicity of an element in a multiset.
math.setPowerset(set)	Create the powerset of a (multi)set.
math.setSize(set)	Count the number of elements of a (multi)set.
math.setSymDifference(set1, set2)	Create the symmetric difference of two (multi)sets.
math.setUnion(set1, set2)	Create the union of two (multi)sets.